Variáveis contínuas
Crie um novo projeto no RStudio e coloque na pasta os arquivos
corpus.csvedados.csv. Crie umscriptdo Rstudio para registrar a sua análise. Com esse procedimento, não será necessário ficar mudando de diretório. E você pode voltar os passos caso tenha dificuldade com um comando. Este símbolo#significa que oscriptnão irá ler o que está na sequência; utilize para inserir comentários sobre sua análise.
Vamos trabalhar com variáveis quantitativas. Para isso, vamos usar o conjunto de dados do capítulo Palavras-tabu e efeitos de gênero na leitura (Pinheiro, Menezes & Freitag, 2020), que apresenta o resultado de um estudo sobre os efeitos de palavras-tabu e de gênero na situação de leitura como pistas de processamento de estereótipo e preconceito.
A organização de um conjunto de dados depende da pergunta que será feita a eles. Por isso, é importante ter clareza das perguntas a serem feitas antes de iniciar a coleta, para não trabalhar à toa. Existem duas formas de organizar os dados, e elas podem ser manipuladas com os recursos do pacote dplyr. Os dados podem ser pareados ou alinhados.
Importar os dados
Este arquivo apresenta as variáveis pareadas. Vamos importar da tabela em formato *.csv para o formato de dataframe do R:
dados <- read.table("dados.csv", sep = ";", header = T) Observe a estrutura do conjunto de dados importado:
str(dados)
#> 'data.frame': 40 obs. of 6 variables:
#> $ participante : chr "lili" "lili" "luana" "luana" ...
#> $ entrevistador : chr "homem" "homem" "homem" "homem" ...
#> $ tempo.de.leitura: num 0.92 0.54 0.52 1.62 0.43 0.71 1.09 0.71 0.46 1.02 ...
#> $ tipo.de.texto : chr "texto um" "texto dois" "texto um" "texto dois" ...
#> $ sexo : chr "feminino" "feminino" "feminino" "feminino" ...
#> $ metacomentario : chr "nao" "nao" "nao" "sim" ...Observe que são dois tipos de variáveis: factor e num. Estas são as seis primeiras ocorrências do conjunto de dados:
head(dados)
#> participante entrevistador tempo.de.leitura tipo.de.texto sexo
#> 1 lili homem 0.92 texto um feminino
#> 2 lili homem 0.54 texto dois feminino
#> 3 luana homem 0.52 texto um feminino
#> 4 luana homem 1.62 texto dois feminino
#> 5 mariane homem 0.43 texto um feminino
#> 6 mariane homem 0.71 texto dois feminino
#> metacomentario
#> 1 nao
#> 2 nao
#> 3 nao
#> 4 sim
#> 5 nao
#> 6 naoE estas são as cinco últimas ocorrências:
tail(dados)
#> participante entrevistador tempo.de.leitura tipo.de.texto sexo
#> 35 joao mulher 0.94 texto um masculino
#> 36 joao mulher 0.64 texto dois masculino
#> 37 jose mulher 0.99 texto um masculino
#> 38 jose mulher 0.95 texto dois masculino
#> 39 eduardo mulher 1.00 texto um masculino
#> 40 eduardo mulher 1.15 texto dois masculino
#> metacomentario
#> 35 nao
#> 36 nao
#> 37 nao
#> 38 nao
#> 39 nao
#> 40 naofactor é uma variável qualitativa e num é uma variável quantitativa. Este comando apresenta um resumo das variáveis:
summary(dados)
#> participante entrevistador tempo.de.leitura tipo.de.texto
#> Length:40 Length:40 Min. :0.4300 Length:40
#> Class :character Class :character 1st Qu.:0.5775 Class :character
#> Mode :character Mode :character Median :0.9400 Mode :character
#> Mean :0.8460
#> 3rd Qu.:1.0000
#> Max. :1.6200
#> sexo metacomentario
#> Length:40 Length:40
#> Class :character Class :character
#> Mode :character Mode :character
#>
#>
#> Agora, vamos ver outro arranjo para os mesmos dados. Vamos importar este arquivo, que apresenta as variáveis alinhadas.
corpus <- read.table("corpus.csv", sep = ";", header = T)Faça o mesmo que fez com o arquivo anterior.
summary(corpus)
#> participante texto.1 metacomentario texto.2
#> Length:20 Min. :0.5400 Length:20 Min. :0.430
#> Class :character 1st Qu.:0.9675 Class :character 1st Qu.:0.500
#> Mode :character Median :1.0550 Mode :character Median :0.735
#> Mean :1.0845 Mean :0.743
#> 3rd Qu.:1.2325 3rd Qu.:0.985
#> Max. :1.6200 Max. :1.170
#> entrevistador sexo
#> Length:20 Length:20
#> Class :character Class :character
#> Mode :character Mode :character
#>
#>
#> Compare o resumo de variáveis dos dois conjuntos de dados: qual a diferença entre eles? Observe que a forma como organizamos nosso conjunto de dados pode interferir nos tipos de resposta que precisamos. Dito de outra forma: o modo como organizamos o conjunto de dados deve favorecer o tipo de respostas que precisamos dos dados. Por isso, vale a pena repetir: antes de sair coletando dados, é preciso ter clareza das perguntas que serão feitas aos dados!
Inspecionar os dados
Primeiro, é preciso carregar os pacotes para manipulação dos dados. Instale antes. Cada um executará uma função específica e tutoriais para seu uso podem ser encontrados facilmente. Recomendo que estudem os pacotes e vejam as possibilidade de maniputação.
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
library(report)
library(ggplot2)
library(ggsignif)
library(forcats)
library(ggpubr)
#> Loading required package: magrittr
library(rstatix)
#>
#> Attaching package: 'rstatix'
#> The following object is masked from 'package:stats':
#>
#> filterUma pergunta que precisamos fazer aos dados é se existe diferença no tempo de leitura entre os textos e se essa diferença é significativa.
A primeira pergunta pode ser respondida com a função summary(). Para dizer se essa diferença é signficativa, precisamos realizar um teste estatístico de significância para a diferença. Antes de decidir pelo teste, precisamos conhecer os dados.
A distribuição é normal?
Por inspeção visual, podemos ver se há normalidade. Para isso, fazemos um histograma da distribuição dos tempos de leitura, para cada um dos textos (data.frame corpus)
hist(corpus$texto.1, main = "Histograma para normalidade dos dados \ texto 1")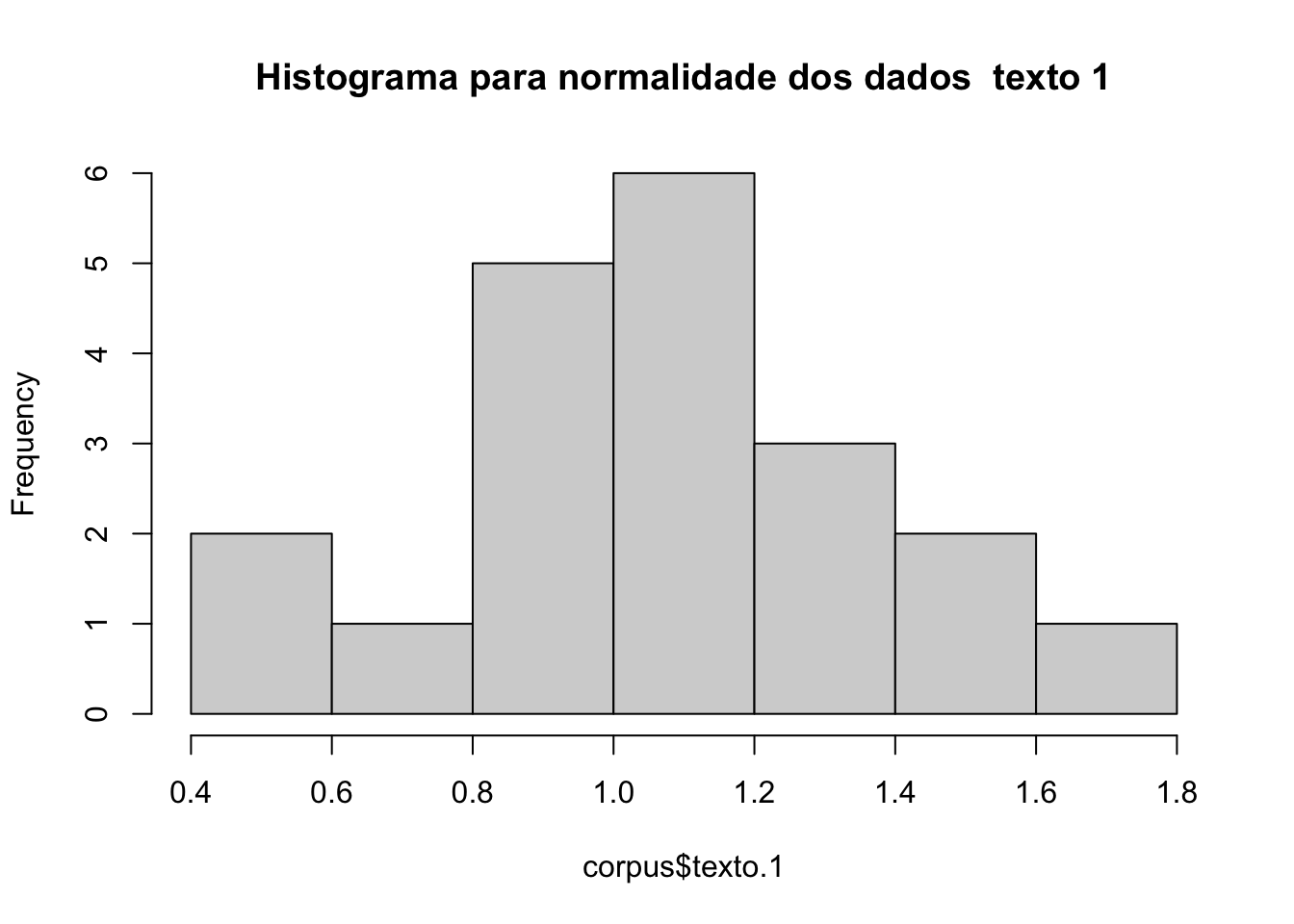
Visualmente, conseguimos ver uma curva normal nos dados. Vamos fazer um teste Shapiro. A hipótese nula do teste de Shapiro-Wilk é que a população tem distribuição normal. Portanto, um valor de p < 0.05 indica que a hipótese nula é rejeitada, ou seja, os dados não apresentam distribuição normal.
shapiro.test(corpus$texto.1)
#>
#> Shapiro-Wilk normality test
#>
#> data: corpus$texto.1
#> W = 0.96974, p-value = 0.7493Os dados têm distribuição normal. A dispersão pode ser visualizada:
ggqqplot(corpus$texto.1)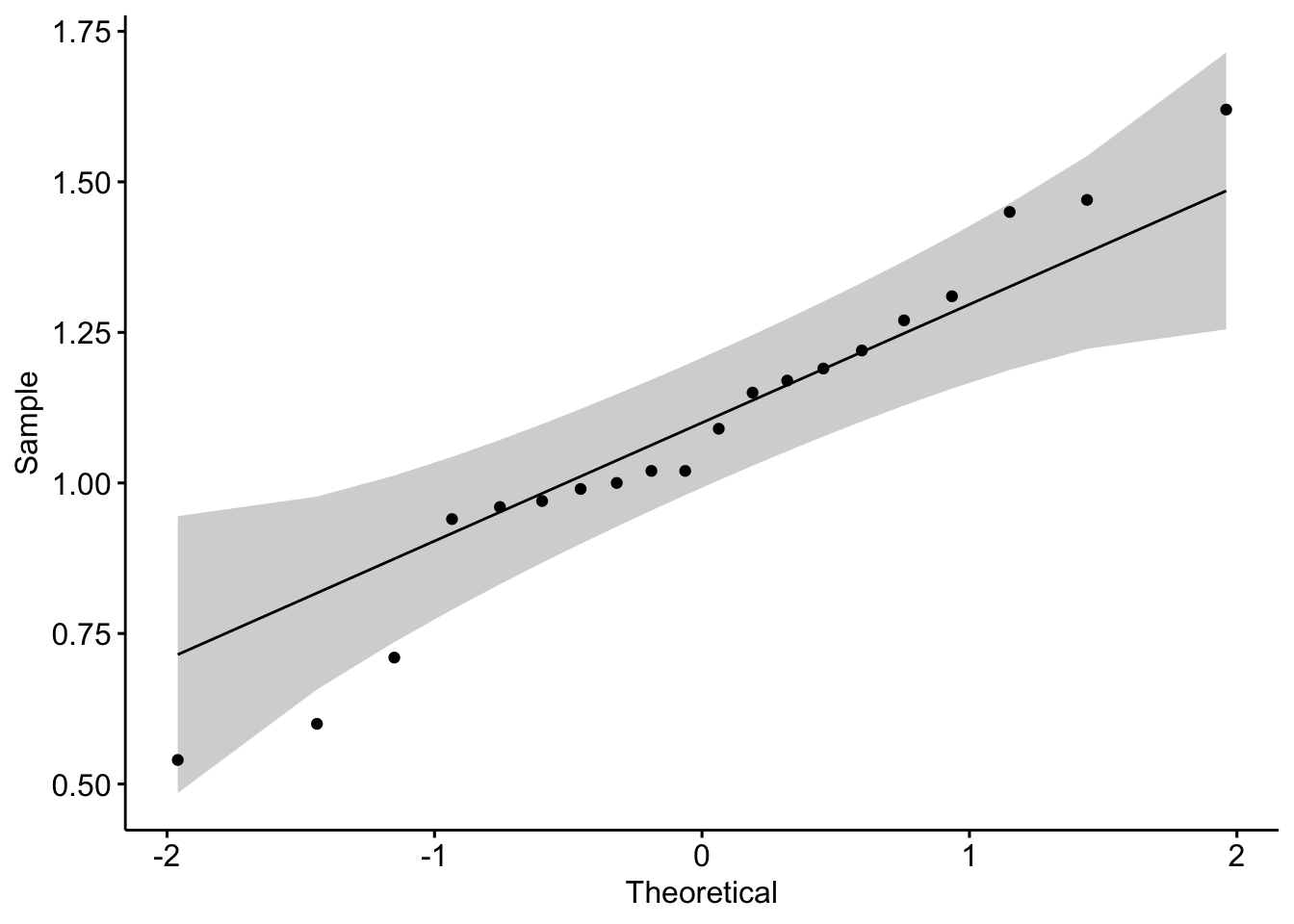
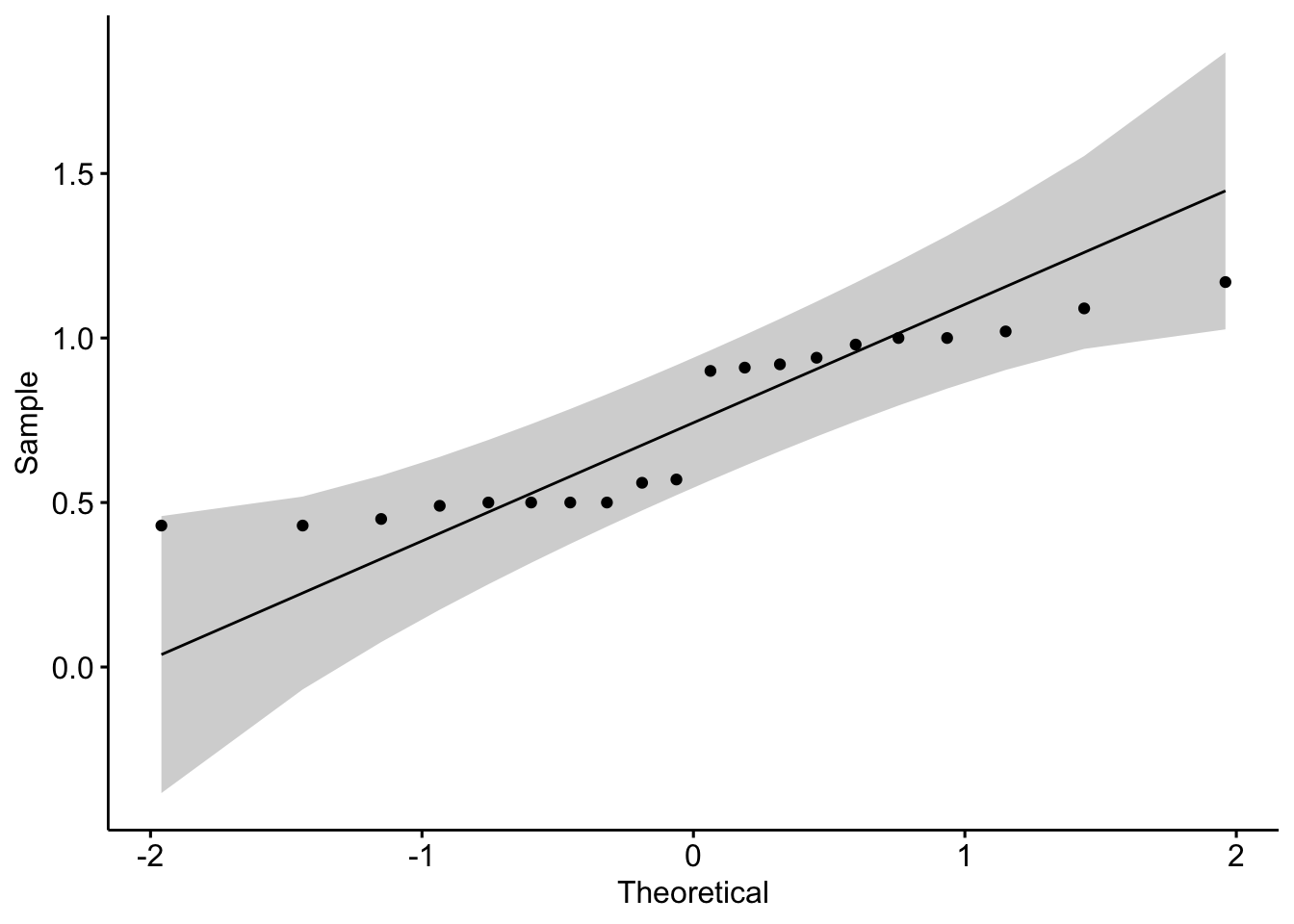
Agora faça o mesmo para o texto 2; a distribuição é normal? 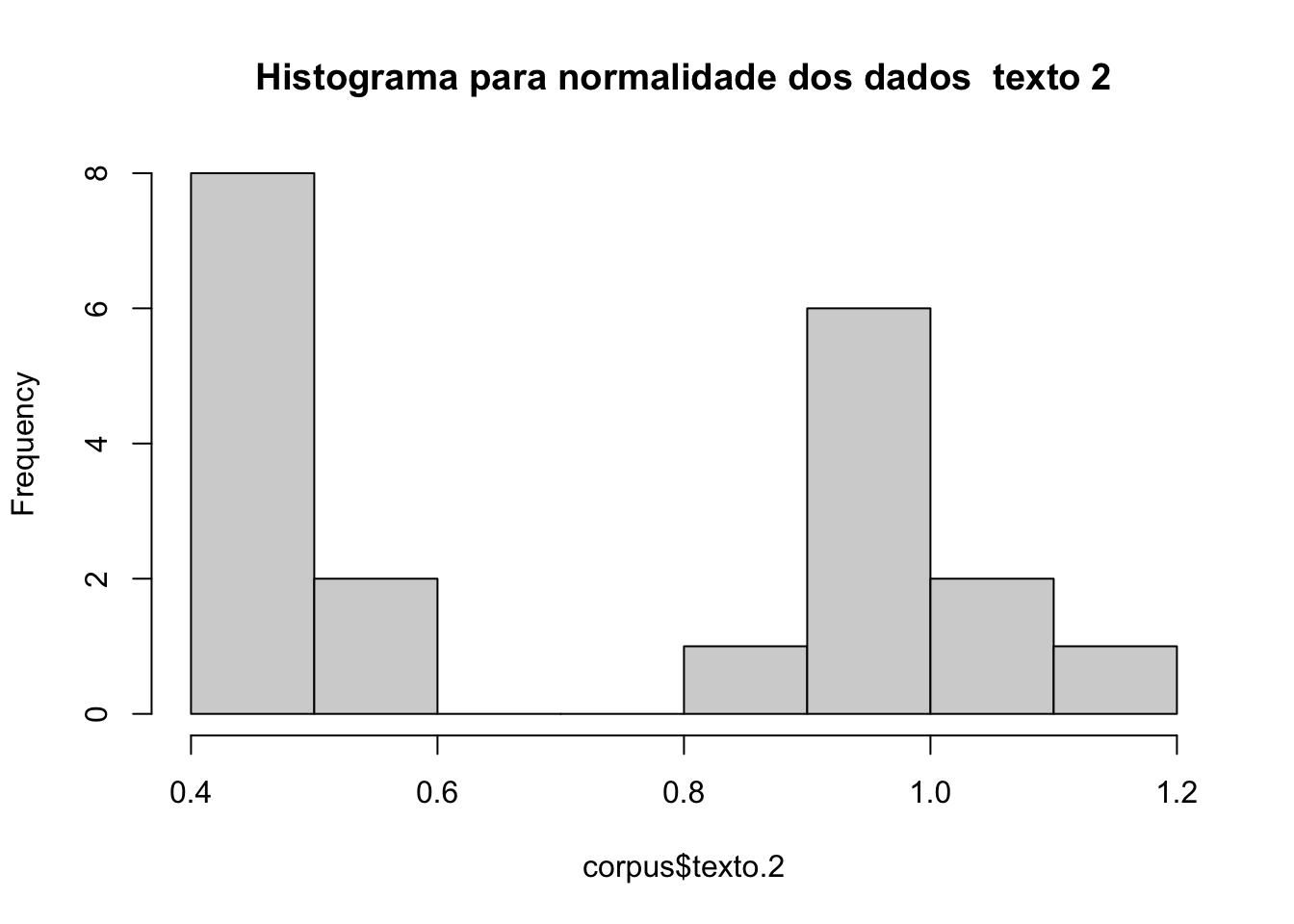
#>
#> Shapiro-Wilk normality test
#>
#> data: corpus$texto.2
#> W = 0.8365, p-value = 0.003193A amostra é muito pequena (20 participantes); certamente, a ampliação da amostra resolveria o problema…
A variância é homogênea?
Vamos testar a homogeneidade da variância entre os grupos. Aplicaremos o teste Bartlett, que : hipótese nula é que não há diferença na variância entre grupos. Para isso, será preciso testar o efeito de cada grupo (variável independente nominal, no caso, sexo do participante e sexo do entrevistador) em cada texto:
bartlett.test(texto.1 ~ entrevistador, data = corpus)
#>
#> Bartlett test of homogeneity of variances
#>
#> data: texto.1 by entrevistador
#> Bartlett's K-squared = 4.3025, df = 1, p-value = 0.03806
bartlett.test(texto.2 ~ entrevistador, data = corpus)
#>
#> Bartlett test of homogeneity of variances
#>
#> data: texto.2 by entrevistador
#> Bartlett's K-squared = 0.0026807, df = 1, p-value = 0.9587
bartlett.test(texto.1 ~ sexo, data = corpus)
#>
#> Bartlett test of homogeneity of variances
#>
#> data: texto.1 by sexo
#> Bartlett's K-squared = 2.1265, df = 1, p-value = 0.1448
bartlett.test(texto.2 ~ sexo, data = corpus)
#>
#> Bartlett test of homogeneity of variances
#>
#> data: texto.2 by sexo
#> Bartlett's K-squared = 0.010829, df = 1, p-value = 0.9171Observe os resultados e diga qual é o grupo que está inteferindo na variância?
Há correlação entre as variáveis?
A próxima inspeção é saber se correlação entre os dados, ou seja, se há interferência de uma variável na outra. Nos termos do objetivo do estudo em questão, precisamos saber se o tempo de leitura do texto 1 interfere no texto de leitura do texto 2.
Para isso, vamos calcular o coeficiente de correlação, que mede se e o quanto duas variáveis quantitativas tendem a mudar juntas. Existem três testes, cada um com sua especificidade de variáveis: O coeficiente de correlação de Pearson (r) mede o grau da correlação linear entre duas variáveis quantitativas numéricas. Quando as variáveis são ordinais, podem ser considerados os coeficientes de correlação de Spearman ρ (rhô) ou de Kendall τ (tau); a estatística do teste Kendall é mais robusta, porém, é sensível a amostras restritas. O coeficiente de correlação pode variar de -1 a +1, quanto maior for o valor absoluto do coeficiente, mais forte é a relação entre as variáveis. Um valor absoluto de 1 indica uma relação perfeita, e um valor zero indica ausência de relação. Para realizar o teste, utilizamos a função cor.test e especificamos o método:
cor.test(corpus$texto.1, corpus$texto.2,
method = "spearman")
#> Warning in cor.test.default(corpus$texto.1, corpus$texto.2, method =
#> "spearman"): Cannot compute exact p-value with ties
#>
#> Spearman's rank correlation rho
#>
#> data: corpus$texto.1 and corpus$texto.2
#> S = 753.68, p-value = 0.05631
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0.4333245O resultado do teste nos permite dizer que, embora o tempo de leitura seja diferente entre os textos, não há correlação entre eles.
Vamos fazer a inspeção visual do resultado; se a hipótese de pesquisa considerasse a correlação, esta figura poderia ser incluída na análise.
ggscatter(corpus, y = "texto.1", x = "texto.2",
add = "reg.line", conf.int = FALSE,
cor.coef = TRUE, cor.method = "spearman",
ylab = "Tempo de leitura texto 1", xlab = "Tempo de leitura texto 2")
#> `geom_smooth()` using formula 'y ~ x'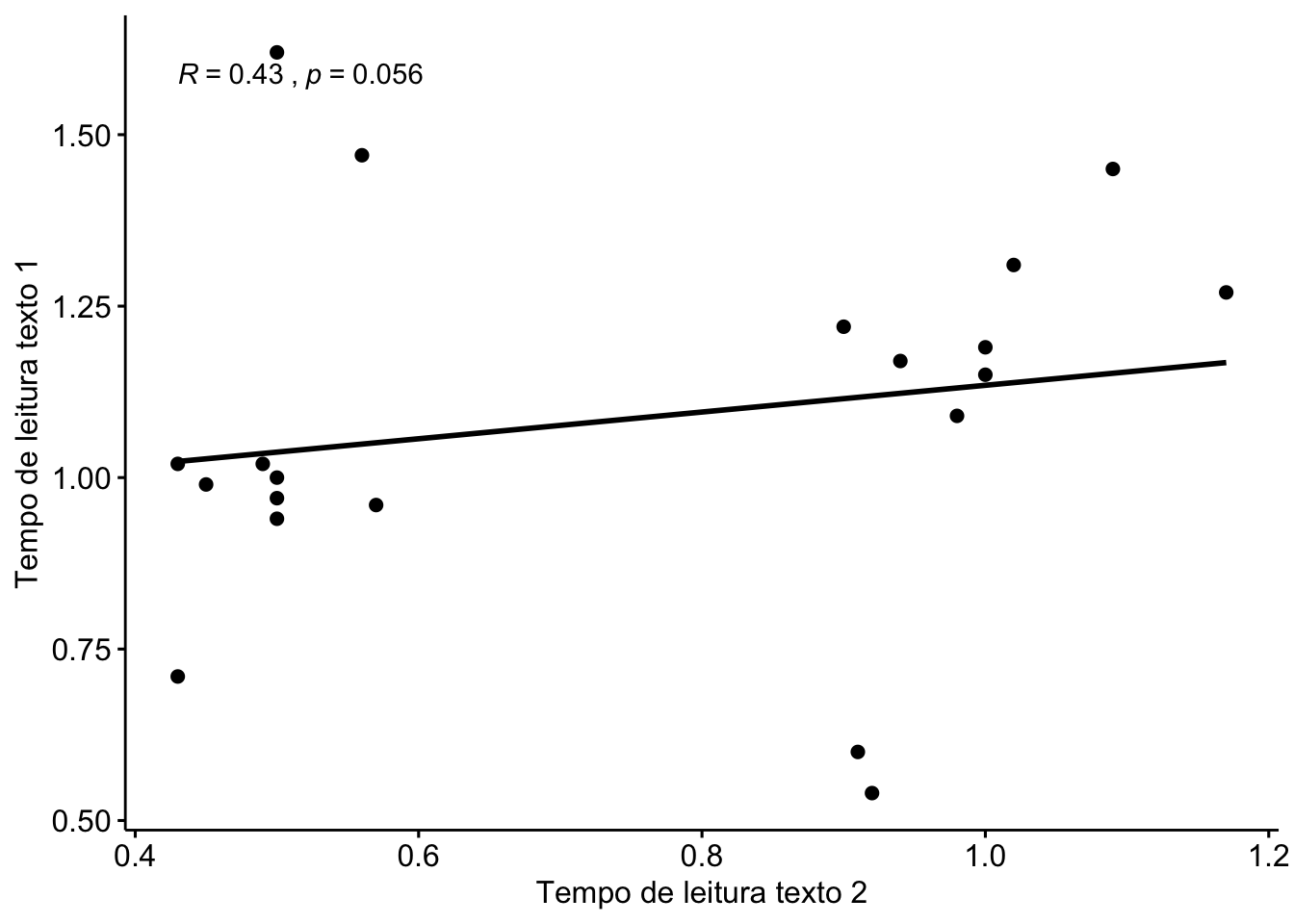
Já testamos a normalidade da distribuição e a correlação entre as variáveis. A partir disso, podemos escolher que teste estatístico aplicaremos para explicar a diferença na comparação entre as médias de tempo de leitura em cada um dos textos.
Comparação de médias
Para comparar médias, podemos utilizar um conjunto de testes, a depender da quantidade de grupos e do tipo de distribuição dos dados. Neste tutorial, vamos conhecer os usos dos testes: T, Wilcoxon, ANOVA e Kruskal-Wallis.
Para selecionar o teste, precisamos saber o que queremos fazer:
- Comparar a média de uma amostra com uma média já conhecida?
- Comparar as médias de dois grupos independentes?
- Comparar as médias de dois grupos pareados?
- Comparar as médias de mais de dois grupos?
Vamos trabalhar neste tutorial os três primeiros casos.
Comparar a média de uma amostra com uma média já conhecida
Sejam corpus e dados resultados de dois estudos distintos. A média do tempo de leitura de dados pode ser calculada da seguinte forma:
mean(dados$tempo.de.leitura)
#> [1] 0.846Queremos saber qual a relação entre o tempo de leitura de dados e o tempo leitura de texto.1 em corpus.
Primeiro, precisamos testar a normalidade dos dados. Teste a normalidade da distribuição de texto.1 em corpus:
shapiro.test(corpus$texto.1)
#>
#> Shapiro-Wilk normality test
#>
#> data: corpus$texto.1
#> W = 0.96974, p-value = 0.7493Como a distribuição é normal, podemos realizar um teste-t para uma amostra. Este é um teste paramétrico, que pressupõe a condição de normalidade dos dados. Temos a média, calculada por mean(dados$tempo.de.leitura). Podemos querer saber se a média do tempo de leitura em corpus$texto.1 é igual, menor ou maior do que um valor conhecido assumido como padrão de referência (no caso, dados$tempo.de.leitura).
Vamos fazer o teste assumindo a hipótese de que a média de corpus$texto.1 será igual à média teórica/já conhecida (mu), assumindo um nível de alfa = 0.05:
t.test(corpus$texto.1, mu = 0.846, alternative = "two.side")
#>
#> One Sample t-test
#>
#> data: corpus$texto.1
#> t = 3.8734, df = 19, p-value = 0.001023
#> alternative hypothesis: true mean is not equal to 0.846
#> 95 percent confidence interval:
#> 0.9556251 1.2133749
#> sample estimates:
#> mean of x
#> 1.0845Agora vamos fazer o mesmo procedimento de comparação da média de dados$tempo.de.leitura com texto.2. Precisamos saber se a amostra satisfaz as condições de normalidade.
shapiro.test(corpus$texto.2)
#>
#> Shapiro-Wilk normality test
#>
#> data: corpus$texto.2
#> W = 0.8365, p-value = 0.003193Como a distribuição não atende às condições de normalidade, precisamos utilizar um teste equivalente não-paramétrico, o teste Wilcoxon para uma amostra. Este teste permite determinar se a mediana de uma amostra é igual, maior ou menor do que um valor conhecido assumido como padrão de referência.
Média e mediana são medidas de tendência central e só se aplicam a variáveis quantitativas.
- Média: somatório de todos os elementos da série dividido pelo número de elementos.
- Mediana: metade do valor central (ordenação crescente dos elementos dividida em duas partes).
Vamos calcular a mediana de texto.2:
median(corpus$texto.2)
#> [1] 0.735Agora que sabemos a mediana, o procedimento é o mesmo do teste-t, só que com a função wilcox.test(). Vamos testar a hipótese de que são iguais:
wilcox.test(corpus$texto.2, mu = 0.735, alternative = "two.side")
#> Warning in wilcox.test.default(corpus$texto.2, mu = 0.735, alternative =
#> "two.side"): cannot compute exact p-value with ties
#>
#> Wilcoxon signed rank test with continuity correction
#>
#> data: corpus$texto.2
#> V = 110, p-value = 0.8664
#> alternative hypothesis: true location is not equal to 0.735Em resumo, quando temos uma amostra e queremos comparar com um valor já conhecido, primeiro testamos a normalidade dos dados. Se os dados apresentam distribuição normal, escolhemos o teste-T para uma amostra, um teste paramétrico; se as condições de normalidade não são atendidas, escolhemos o teste Wilcoxon para uma amostra, um teste não paramétrico.
Comparar as médias de dois grupos independentes
Queremos saber se o tempo de leitura de participantes homens é diferente do tempo de leitura de participantes mulheres no texto.1. Temos dois grupos independentes entre si, e esta identificação é importante para os procedimentos de seleção dos testes estatísticos.
Já sabemos que os dados de texto.1 têm distribuição normal; vamos ver se a normalidade se conserva dentro dos grupos:
# teste Shapiro para normalidade com dados de participantes homens
with(corpus, shapiro.test(texto.1[sexo == "masculino"]))
#>
#> Shapiro-Wilk normality test
#>
#> data: texto.1[sexo == "masculino"]
#> W = 0.89336, p-value = 0.1849
# teste Shapiro para normalidade com dados de participantes mulheres
with(corpus, shapiro.test(texto.1[sexo == "feminino"]))
#>
#> Shapiro-Wilk normality test
#>
#> data: texto.1[sexo == "feminino"]
#> W = 0.95066, p-value = 0.6763Como os grupos da amostra atendem às condições de normalidade e homogeneidade, podemos empregar um teste paramétrico, o teste-t para amostras independentes para saber se a média entre os grupos é igual, maior ou menor. Vamos testar se as médias são iguais (`alternative = “two.side”’).
t.test(texto.1 ~ sexo, data = corpus, var.equal = TRUE, alternative = "two.side")
#>
#> Two Sample t-test
#>
#> data: texto.1 by sexo
#> t = 0.1186, df = 18, p-value = 0.9069
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.2507083 0.2807083
#> sample estimates:
#> mean in group feminino mean in group masculino
#> 1.092 1.077A última linha do teste informa a média de cada grupo. Vamos fazer a mesma pergunta sobre o efeito dos participantes ao texto.2: existe diferença no tempo de leitura de participantes homnes e participantes mulheres? Em não sendo satisfeita a condição de normalidade entre os grupos, utilizamos um teste não paramétrico, o teste de Wilcoxon para amostras independentes. A sintaxe do teste é a mesma do teste-t. Vamos testar a hipótese de que a mediana do tempo de leitura de participantes mulheres será maior do que a de participantes homens:
wilcox.test(texto.2 ~ sexo, data = corpus,
exact = FALSE, alternative = "greater")
#>
#> Wilcoxon rank sum test with continuity correction
#>
#> data: texto.2 by sexo
#> W = 34, p-value = 0.8949
#> alternative hypothesis: true location shift is greater than 0Comparar as médias de dois grupos pareados
Agora chegamos ao objetivo do estudo em questão: um mesmo participante, leu dois textos diferentes. Temos a mesma medida para cada participante, é o que chamamos de amostras dependentes ou pareadas. Os testes a serem realizados são os mesmos apresentados anteriormente, teste-t para amostras pareadas, se a condição de normalidade é atendida, ou teste Wilcoxon para amostras pareadas se a condição de normalidade não é atendida.
Já sabemos que em dados$tempo.de.leitura a distribuição não é normal.
shapiro.test(dados$tempo.de.leitura)
#>
#> Shapiro-Wilk normality test
#>
#> data: dados$tempo.de.leitura
#> W = 0.91501, p-value = 0.005386Porém, todos os trabalhos com leitura sempre sinalizam para a normalidade das distribuições. Uma explicação para essa amostra seria o tamanho; se ampliássemos o número de participantes, a normalidade tenderia a se regularizar. Outra possibilidade é erro no cômputo de algum dado, um zero a mais ou a menos, uma mudança de ordem de algarismo na hora da digitação. Por isso é importante realizar a inspeção dos dados; sempre que algo sair do que é esperado a partir das evidências de outros estudos, deve-se checar a possível interferência.
Um primeiro procedimento a ser feito é o de inspeção de outliers, distribuições fora dos parâmetros.
dados %>%
group_by(tipo.de.texto, sexo, entrevistador) %>%
identify_outliers(tempo.de.leitura)
#> # A tibble: 5 x 8
#> entrevistador tipo.de.texto sexo participante tempo.de.leitura metacomentario
#> <chr> <chr> <chr> <chr> <dbl> <chr>
#> 1 homem texto dois femi… luana 1.62 sim
#> 2 mulher texto dois masc… joao 0.64 nao
#> 3 mulher texto dois masc… eduardo 1.15 nao
#> 4 mulher texto um femi… vanessa 1 nao
#> 5 homem texto um masc… hugo 0.43 nao
#> # … with 2 more variables: is.outlier <lgl>, is.extreme <lgl>As duas últimas colunas do resultado informam se há valores outlier (is.outlier) e se estes são extremos (is.extreme). Como podemos ver, há três valores extremos (TRUE). Podemoes excluir estes dados para tentar normalizar a análise (mas perderemos 3 participantes).
dados %>%
filter((tipo.de.texto != "Texto-controle" & participante != "vanessa") & (tipo.de.texto != "Texto-controle" & participante != "hugo") | (tipo.de.texto != "Texto-alvo" & participante != "joao")) %>%
identify_outliers(tempo.de.leitura)
#> [1] participante entrevistador tempo.de.leitura tipo.de.texto
#> [5] sexo metacomentario is.outlier is.extreme
#> <0 rows> (or 0-length row.names)dados %>%
filter((tipo.de.texto != "Texto-controle" & participante != "vanessa") & (tipo.de.texto != "Texto-controle" & participante != "hugo") | (tipo.de.texto != "Texto-alvo" & participante != "joao")) %>%
shapiro_test(tempo.de.leitura)
#> # A tibble: 1 x 3
#> variable statistic p
#> <chr> <dbl> <dbl>
#> 1 tempo.de.leitura 0.915 0.00539Para fins didáticos, vamos realizar as análises considerando o teste-t e o teste Wilcoxon. Na prática, as diferenças são poucas. Apenas o procedimento de cálculo muda em função das pressuposições, assim como o modo de reportar os resultados.
Vamos retomar as estatísticas sumárias, com a função get_summary_stats() do pacote rstatixc:
dados %>%
group_by(tipo.de.texto, sexo, entrevistador) %>%
get_summary_stats(tempo.de.leitura)
#> # A tibble: 8 x 16
#> entrevistador tipo.de.texto sexo variable n min max median q1
#> <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 homem texto dois femi… tempo.d… 5 0.54 1.62 0.71 0.71
#> 2 mulher texto dois femi… tempo.d… 5 0.96 1.47 0.99 0.97
#> 3 homem texto dois masc… tempo.d… 5 0.6 1.09 1 0.6
#> 4 mulher texto dois masc… tempo.d… 5 0.64 1.15 0.95 0.94
#> 5 homem texto um femi… tempo.d… 5 0.43 1.09 0.52 0.46
#> 6 mulher texto um femi… tempo.d… 5 0.45 1 0.56 0.5
#> 7 homem texto um masc… tempo.d… 5 0.43 0.98 0.91 0.9
#> 8 mulher texto um masc… tempo.d… 5 0.5 1 0.94 0.580
#> # … with 7 more variables: q3 <dbl>, iqr <dbl>, mad <dbl>, mean <dbl>,
#> # sd <dbl>, se <dbl>, ci <dbl>Além da média (mean) e da mediana (median), que já conhecemos, as estatísticas sumárias incluem outras informações, como:
- Valor mínimo (
min) e valor máximo (max): o menor e o maior valor da série. - Desvio padrão (
sd), uma medida de dispersão: medida do grau de dispersão em relação à média. - Erro padrão (
se): uma medida de estimativa do desvio padrão. - Intervalo de confiança (
ci): estimativa do intervalo considerando o desvio e o erro padrão.
Agora vamos visualizar graficamente essa diferença.
Queremos saber se a diferença de leitura entre os textos é estatisticamente significativa. O texto sem palavras-tabu é o Texto-controle, e o texto com palavras-tabu é o Texto-alvo. Vamos representar graficamente a diferença entre as médias do tempo de leitura, já com o resultado do teste estatístico. Para gerar o gráfico, usamos o pacote ggplot2 e para inserir o teste no gráfico, o pacote ggsignif.
Vamos visualizar o resultado primeiramente com o teste-t:
ggplot(dados, aes(x=tipo.de.texto, y=tempo.de.leitura, fill = tipo.de.texto)) +
geom_boxplot(outlier.shape = NA) +
scale_fill_grey(start = 0.8, end = 0.6) +
geom_jitter(width = .05,
height = 0,
alpha = 0.4) +
theme_minimal() +
theme(legend.position = "none") +
ggtitle("Comparação entre os tempo de leitura dos textos") +
xlab("Textos lidos") + ylab("Tempo de leitura (em minutos)") +
stat_compare_means(method = "t.test", paired = TRUE) ### Informamos que queremos um teste-t, pareado
#> Warning: `select_()` is deprecated as of dplyr 0.7.0.
#> Please use `select()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_warnings()` to see where this warning was generated.
#> Warning: `tbl_df()` is deprecated as of dplyr 1.0.0.
#> Please use `tibble::as_tibble()` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_warnings()` to see where this warning was generated.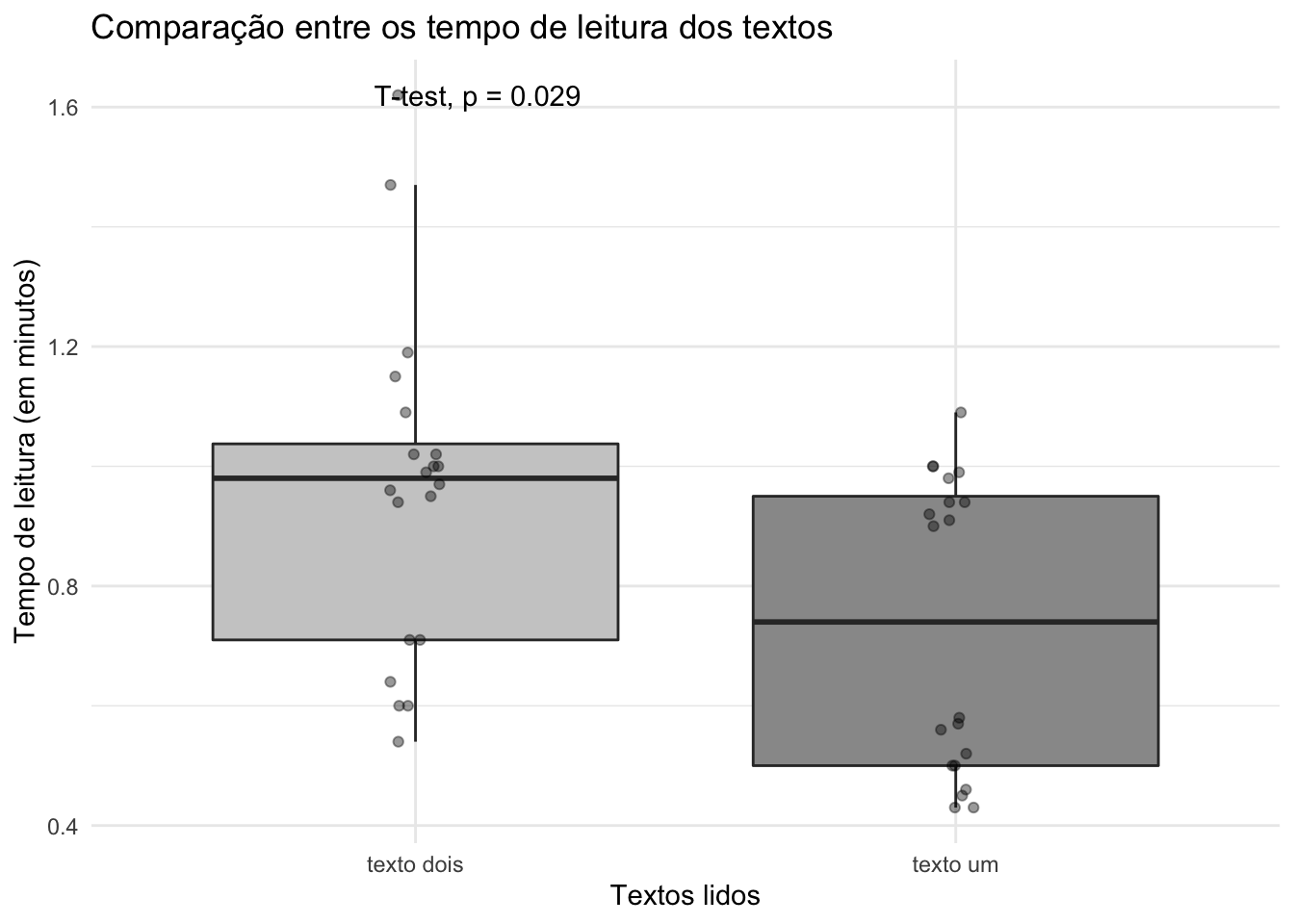
Somente o cálculo do teste:
t.test(dados$tempo.de.leitura ~ dados$tipo.de.texto, paired = TRUE)
#>
#> Paired t-test
#>
#> data: dados$tempo.de.leitura by dados$tipo.de.texto
#> t = 2.3611, df = 19, p-value = 0.02906
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> 0.02554909 0.42445091
#> sample estimates:
#> mean of the differences
#> 0.225Vamos gerar o mesmo gráfico, mas agora com o teste Wilcoxon:
ggplot(dados, aes(x=tipo.de.texto, y=tempo.de.leitura, fill = tipo.de.texto)) +
geom_boxplot(outlier.shape = NA) +
scale_fill_grey(start = 0.8, end = 0.6) +
geom_jitter(width = .05,
height = 0,
alpha = 0.4) +
theme_minimal() +
theme(legend.position = "none") +
ggtitle("Comparação entre os tempo de leitura dos textos") +
xlab("Textos lidos") + ylab("Tempo de leitura (em minutos)") +
stat_compare_means(method = "wilcox.test", paired = TRUE)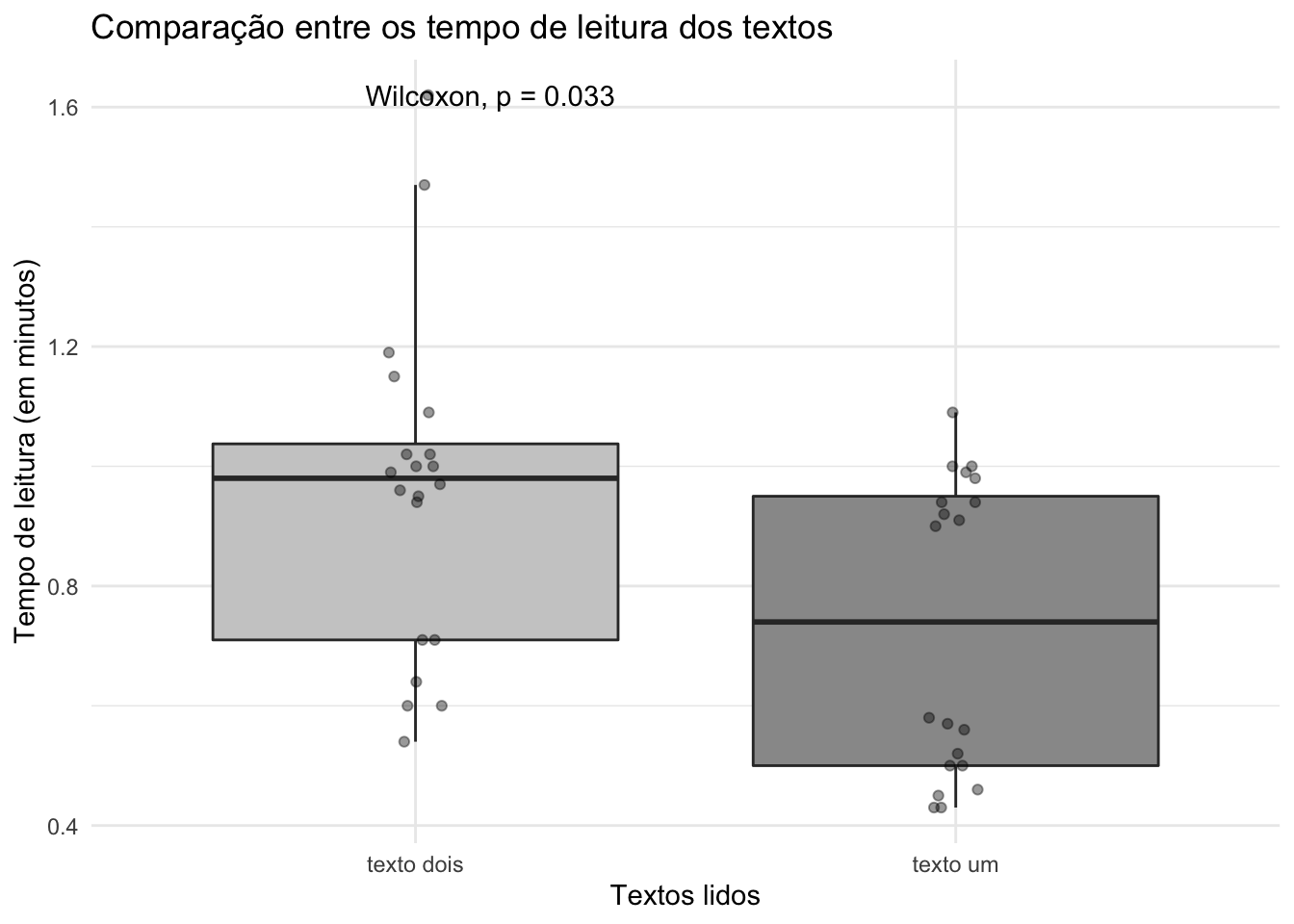
wilcox.test(dados$tempo.de.leitura ~ dados$tipo.de.texto, paired = TRUE)
#>
#> Wilcoxon signed rank exact test
#>
#> data: dados$tempo.de.leitura by dados$tipo.de.texto
#> V = 162, p-value = 0.03277
#> alternative hypothesis: true location shift is not equal to 0Como podemos perceber, ambos os testes permitem rejeitar a hipótese nula de que não há diferença, e nos permite lançar a hipótese alternativa de que existe uma diferença entre o tempo de leitura do texto-controle e o texto-alvo.
Agora vamos verificar se existe efeito do sexo do participante no tempo da leitura. Primeiro, precisamos organizar os fatores, para aparecerem no gráfico.
dados$sexo <- dados$sexo %>%
fct_recode("Mulher" = "feminino", "Homem" = "masculino")
dados$sexo <- factor(dados$sexo, levels = c("Homem", "Mulher")) E vamos gerar o gráfico:
ggplot(dados, aes(x=tipo.de.texto, y=tempo.de.leitura, fill = tipo.de.texto)) +
geom_boxplot(outlier.shape = NA, width = .5) +
scale_fill_grey(start = 0.8, end = 0.6) +
geom_jitter(width = .05,
height = 0,
alpha = 0.4) +
facet_wrap(~sexo) +
theme_minimal() +
theme(legend.position = "none") +
ggtitle("Efeito do sexo do participante no tempo de leitura dos textos") +
xlab("Textos lidos") + ylab("Tempo de leitura (em minutos)") +
stat_compare_means(method = "t.test", paired = TRUE)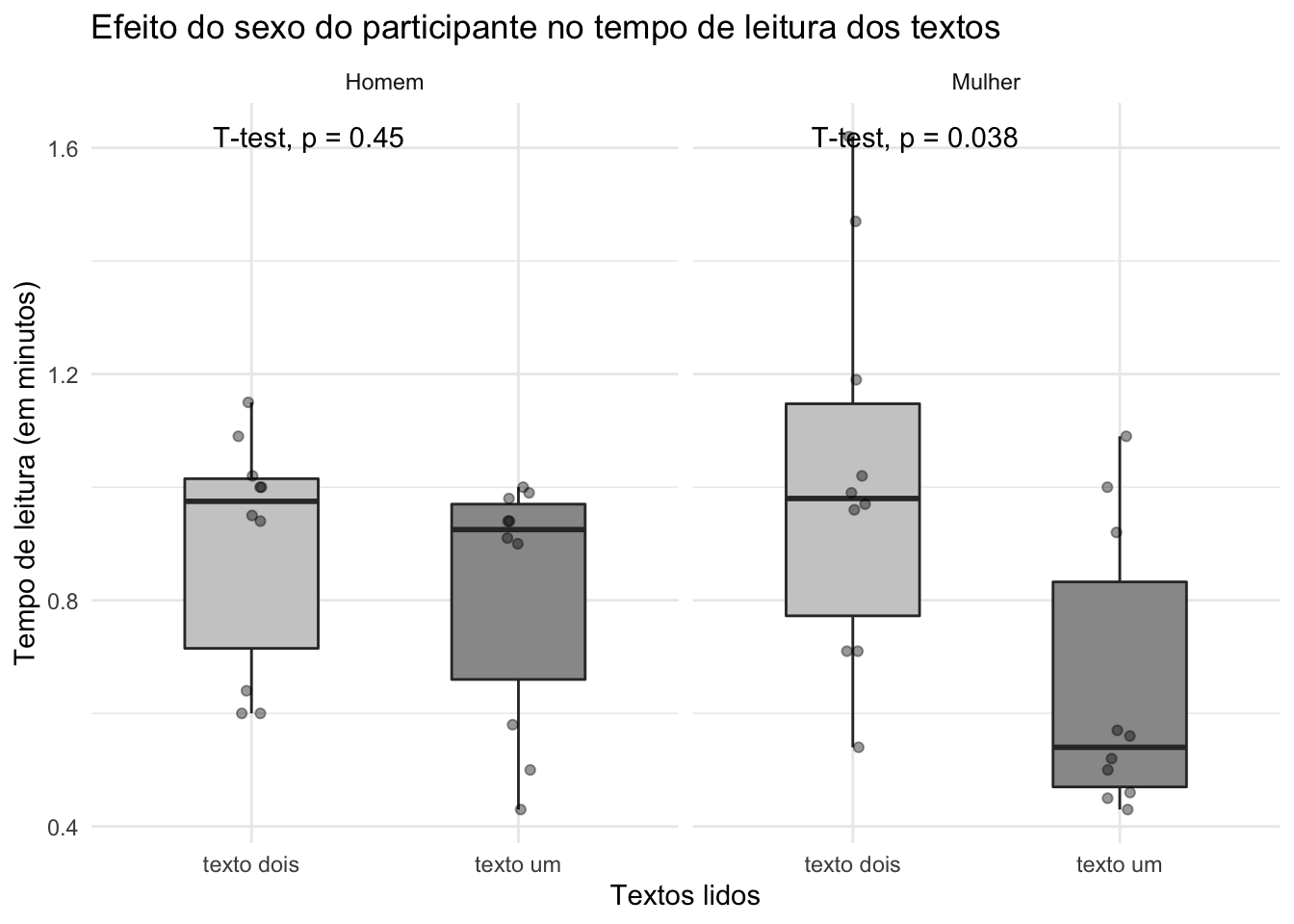
Vamos incorporar ao gráfico uma linha com a média do tempo de leitura:
ggplot(dados, aes(x=tipo.de.texto, y=tempo.de.leitura, fill = tipo.de.texto)) +
geom_hline(yintercept = mean(dados$tempo.de.leitura), linetype = 2) + ### média geral do tempo de leitura
geom_boxplot(outlier.shape = NA, width = .5) +
scale_fill_grey(start = 0.8, end = 0.6) +
geom_jitter(width = .05,
height = 0,
alpha = 0.4) +
facet_wrap(~sexo) +
theme_minimal() +
theme(legend.position = "none") +
ggtitle("Efeito do sexo do participante no tempo de leitura dos textos") +
xlab("Textos lidos") + ylab("Tempo de leitura (em minutos)") +
stat_compare_means(method = "t.test", paired = TRUE)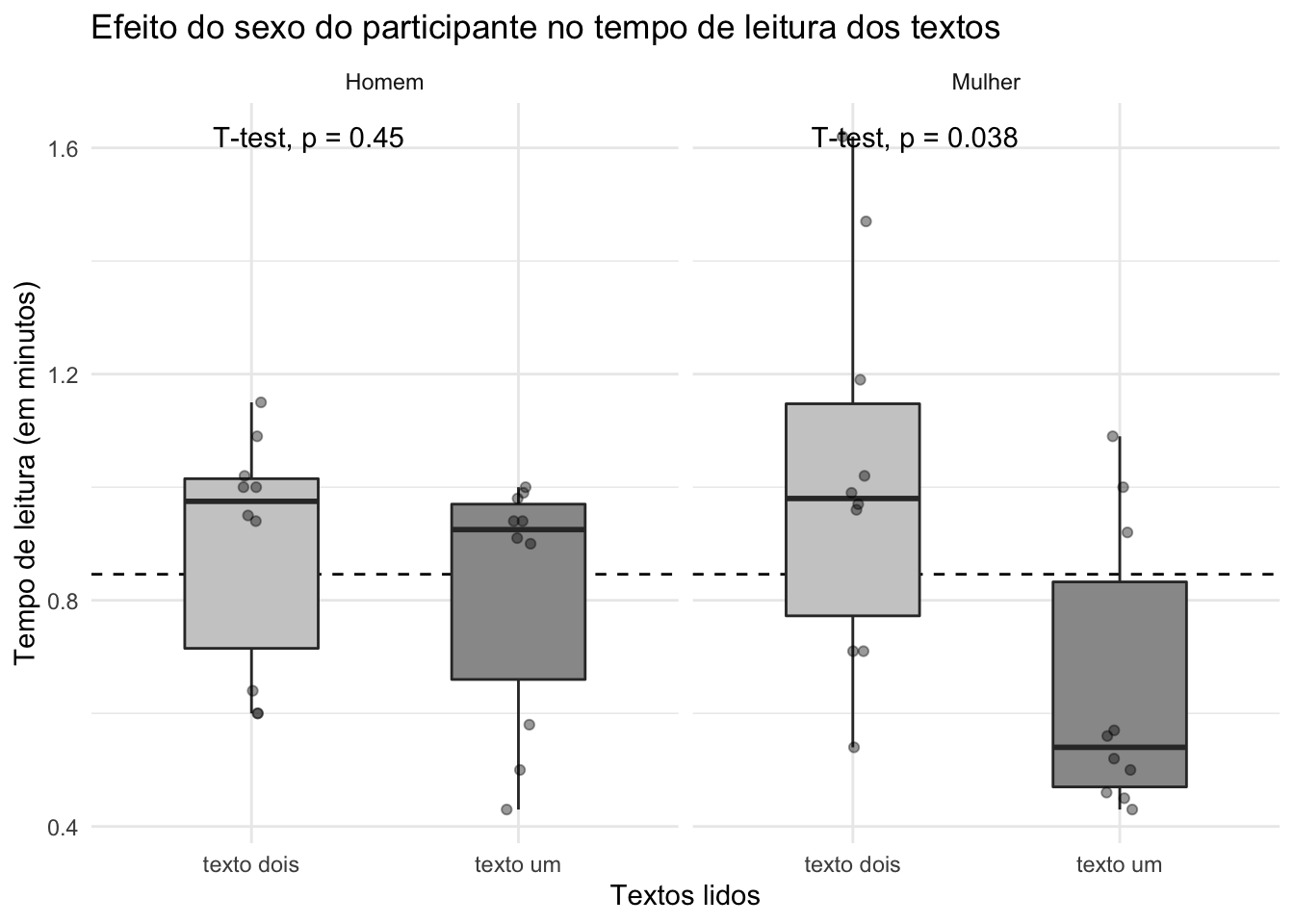
Agora o resultado fica mais claro.
Nossa próxima pergunta é se o sexo do entrevistador interfere no tempo de leitura. Os procedimentos são os mesmos: organizar os fatores, calcular as medidas de centralidade e dispersão, gerar o gráfico, organizar os dados para o teste e realizar o teste para reportar os resultados.
organizar fatores:
dados$entrevistador <- dados$entrevistador %>%
fct_recode("Homem" = "homem", "Mulher" = "mulher")gerar gráfico:
ggplot(dados, aes(x=tipo.de.texto, y=tempo.de.leitura, fill = tipo.de.texto)) +
geom_boxplot(outlier.shape = NA, width = .5) +
scale_fill_grey(start = 0.8, end = 0.6) +
geom_jitter(width = .05,
height = 0,
alpha = 0.4) +
facet_wrap(~ entrevistador) +
theme_minimal() +
theme(legend.position = "none") +
scale_color_manual(labels = c("Texto-controle", "Texto-alvo")) +
ggtitle("Efeito do sexo do entrevistador no tempo de leitura dos textos pelos participantes") +
xlab("Textos lidos") + ylab("Tempo de leitura (em minutos)") +
stat_compare_means(method = "t.test", paired = TRUE)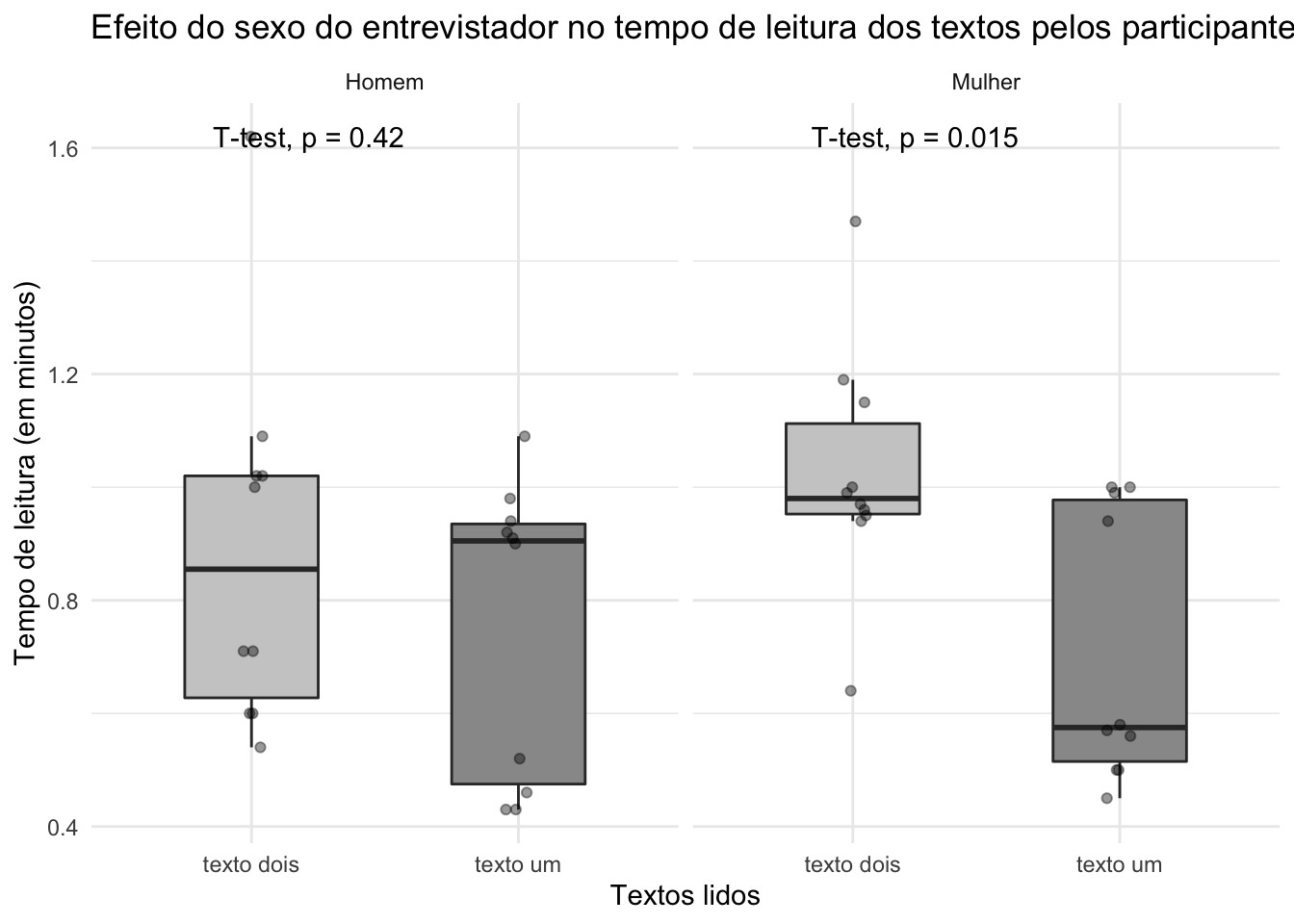
Reportar os resultados
Testes paramétricos comparam médias; testes não paramétricos comparam medianas. Para reportar no corpo do texto os resultados, precisamos das estatísticas sumárias e dos resultados dos testes.
dados %>%
group_by(tipo.de.texto) %>%
get_summary_stats(tempo.de.leitura)
#> # A tibble: 2 x 14
#> tipo.de.texto variable n min max median q1 q3 iqr mad mean
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 texto dois tempo.d… 20 0.54 1.62 0.98 0.71 1.04 0.328 0.208 0.959
#> 2 texto um tempo.d… 20 0.43 1.09 0.74 0.5 0.95 0.45 0.356 0.734
#> # … with 3 more variables: sd <dbl>, se <dbl>, ci <dbl>As estatísticas sumárias são as mesmas. O resultado para o teste-t é
t.test(tempo.de.leitura ~ tipo.de.texto, data = dados, paired = TRUE)
#>
#> Paired t-test
#>
#> data: tempo.de.leitura by tipo.de.texto
#> t = 2.3611, df = 19, p-value = 0.02906
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> 0.02554909 0.42445091
#> sample estimates:
#> mean of the differences
#> 0.225As médias do tempo de leitura do texto-alvo e do texto-controle foram, respectivamente, 0.73 e 0.96 segundos. Um teste-t de amostras pareadas mostra que há um efeito significativo do tipo de texto (t = -2.3611, df = 19, p-valor = 0.029).
wilcox.test(tempo.de.leitura ~ tipo.de.texto, data = dados, paired = TRUE)
#>
#> Wilcoxon signed rank exact test
#>
#> data: tempo.de.leitura by tipo.de.texto
#> V = 162, p-value = 0.03277
#> alternative hypothesis: true location shift is not equal to 0As medianas do tempo de leitura do texto-alvo e do texto-controle foram, respectivamente, 0.74 e 0.98 segundos. Um teste Wilcoxon de amostras pareadas mostra que há um efeito significativo do tipo de texto (V = 48, p-valor = 0.032).
Neste tutorial, vimos o funcionamento de variáveis quantitativas em uma situação pareada e vimos a importância de saber a pergunta que será feita aos dados para poder organizar o conjunto de dados da maneira mais otimizada para as respostas. Aproveite o conhecimento para aplicar em outros estudos! E aprimore seus conhecimentos em dplyr e ggplot2.
Como citar:
FREITAG, Raquel M. K. Variáveis contínuas. Disponível em: https://rkofreitag.github.io/continuas.html/. Acesso em: 2021-04-11.