Replicabilidade na ciência

A ciência vive uma crise generalizada em função da baixa replicabilidade de resultados ou de estudos. Há várias causas para essa crise, uma delas é a falta de clareza de procedimentos de análise dos dados, Como consequência, o poder explanatório das análises e da generalização dos resultados são limitados.

A não explicitação de todos os procedimentos realizados na análise e estatísticas reportadas parcialmente ou apenas quando conveniente são problemas recorrentes nos estudos, o que tornam uma meta-análise muito difícil de ser realizada.

A meta-análise é um procedimento em que são reunidos resultados de estudos com diferentes conjuntos de dado sobre determinado fenômeno e são aplicadas técnicas estatísticas para explicar a variância dos resultados a partir de fatores comuns aos estudos.

Uma vantagem em um estudo de meta-análise é eliminar viéses da revisão da literatura narrativa, em que são reportados resultados de estudo independentemente. Ao integrar as análises, o poder explanatório aumenta.

Vamos explorar neste tutorial algumas estratégias para produzir uma meta-análise, considerando um cenário em que estudos são independentes e com resultados estatísticos reportados apenas parcialmente.

Concordância verbal

A concordância verbal no português brasileiro é um fenômeno amplamente estudado, que tem apresentado resultados convergentes em relação aos condicionamentos internos (saliência fônica, posição), mas diversificados social e dialetalmente. A diversidade tem sido explicada como resultado das diferentes sócio-histórias do português brasileiro. Mas também decorre das diferentes tipologizações dos condicionamentos e por viéses de amostragem.

Vamos examinar os resultados reportados em uma primeira versão de um texto, em que é apresentada uma revisão narrativa da concordância verbal em duas comunidades de fala da Bahia, e aprender a realizar uma meta-análise dos estudos, objeto da segunda versão do texto (em preparação).

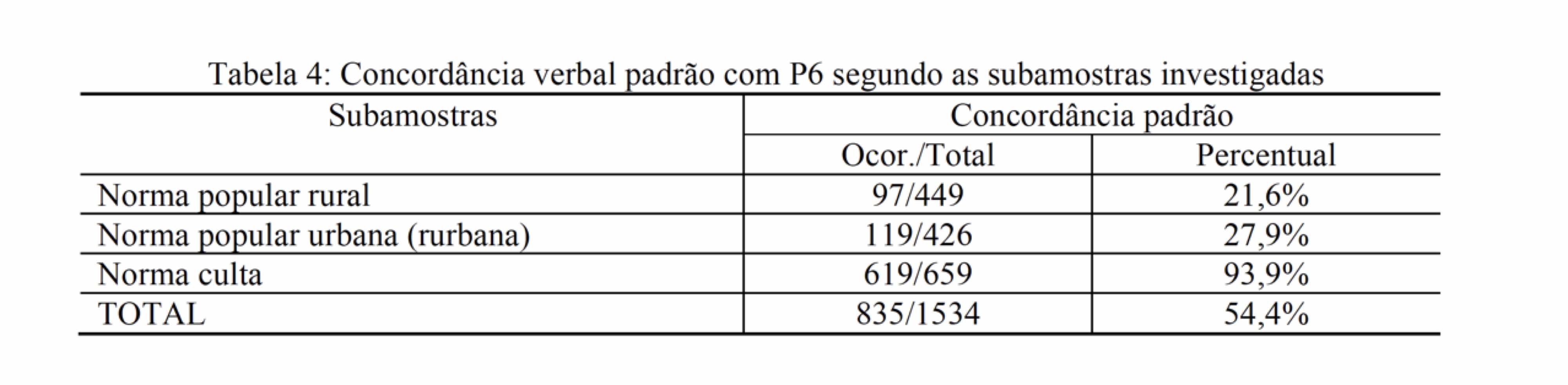
A tabela 2 apresenta a contagem das ocorrências do fenômeno em função do tipo de subamostra. A variável dependente é a realização da concordância, uma variável categórica nominal, e os resultados estão apresentados apenas em função do valor escolhido como default, no caso, a realização padrão. A variável independente é o tipo de amostra, com três níveis, “norma popular rural”, “norma popular urbana” e “norma culta”.

Os percentuais não nos permitem inferências. Um teste inferencial que pode ser realizado é o teste de qui-quadrado, que tem por objetivo verificar se a frequência absoluta observada de uma variável é significativamente diferente da distribuição de frequência absoluta esperada.

Um teste simples que pode ser realizado sem muita dificuldade é o teste aproximado para independência entre as proporções:

aplicacao = c(97, 119, 619)
total = c(449, 436, 659)
prop.test(aplicacao, total, correct = TRUE)
#> 
#>  3-sample test for equality of proportions without continuity
#>  correction
#> 
#> data:  aplicacao out of total
#> X-squared = 738.08, df = 2, p-value < 2.2e-16
#> alternative hypothesis: two.sided
#> sample estimates:
#>    prop 1    prop 2    prop 3 
#> 0.2160356 0.2729358 0.9393020

Se os valores foram digitados corretamente, as proporções apresentadas devem corresponder aos percentuais da tabela. O teste sugere que a distribuição entre as proporções é diferente da hipótese nula (p > 0.001).

Como fazer um teste de qui-quadrado a partir de uma tabela?

  • Informar as variáveis em dois vetores:
    • Um vetor será nomeado de VD e listará os níveis da variável dependente;
    • O outro de VI e listará os níveis da variável independente
  • Listar as contagens de cada nível da variável independente, seguindo a ordem da variável dependente em vetores em uma matriz data.matrix que serão unidos pela função rbind no objeto dadosP6.
  • Vincular os nomes das variáveis:
    • Variável dependente = colnames
    • Variável independente = rownames
VD <- c("concordância", "não concordância")
VI <- c("Norma popular rural", "Norma popular urbana", "Norma culta")
dadosP6 <- data.matrix(rbind(
  c(97, 352),
  c(119, 307),
  c(619, 40)
))
rownames(dadosP6) <- VI
colnames(dadosP6) <- VD

Se todos os procedimentos estiverem corretos, você terá um objeto:

dadosP6
#>                      concordância não concordância
#> Norma popular rural            97              352
#> Norma popular urbana          119              307
#> Norma culta                   619               40

Vamos inspecionar visualmente este objeto, construindo um gráfico de barras:

dadosP6.t = t(dadosP6)      ### Transpor a matriz (colunas em linhas e linhas em colunas)
barplot(dadosP6.t,
        beside = TRUE,      ### Barras lado a lado
        legend = TRUE,
        main = "Frequências da concordância em P6 \n em função do tipo de amostra",
        ylim = c(0, 700),   ### Ajustar o eixo y para o máximo de ocorrências
        cex.names = 0.8,  ### Tamanho do texto das colunas
        cex.axis = 0.8,   ### tamanho do texto dos eixos
        args.legend = list(x   = "topleft",   ### Posição da legenda
                           cex = 0.8,          ### Tamanho do texto da legenda
                           bty = "n"))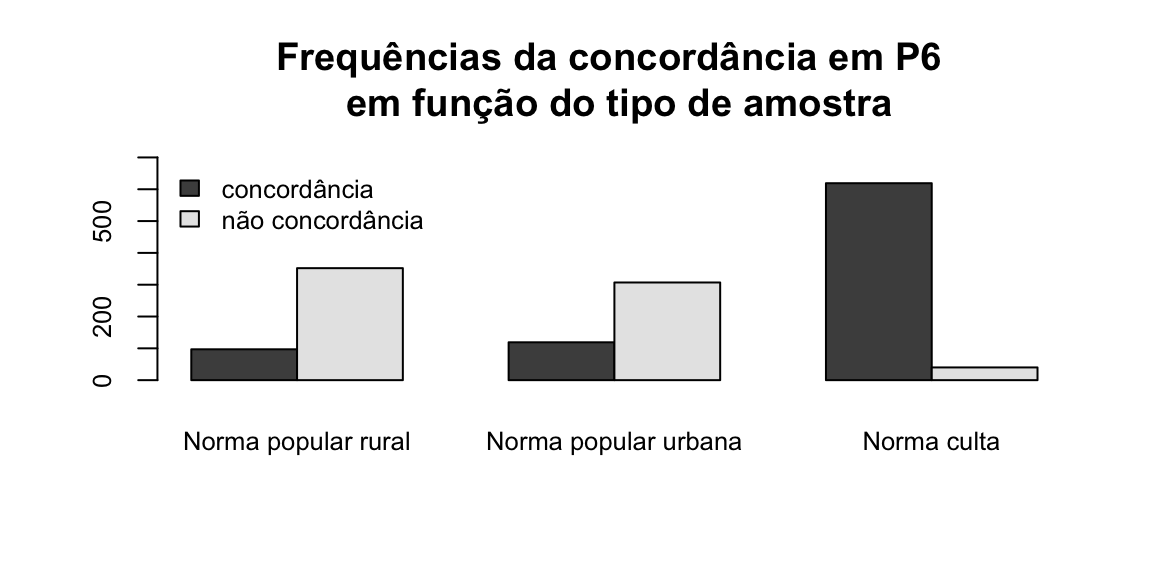

Podemos ver que há uma diferença de distribuição entre os níveis da variável independente.Para confirmar se esta distribuição observada é signficativamente diferente da esperada, realizamos o teste de qui-quadrado:

chisq.test(dadosP6)
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  dadosP6
#> X-squared = 730.18, df = 2, p-value < 2.2e-16

O efeito da dependência é estatisticamente significativo. Podemos descobrir o quanto cada nível contribui para essa associação. Para isso, precisamos investigar os resíduos, ou seja, a diferença entre a frequência observada e a frequência esperada em cada célula.

resultadoP6 <- chisq.test(dadosP6)
round(resultadoP6$residuals, 3)
#>                      concordância não concordância
#> Norma popular rural        -9.429           10.305
#> Norma popular urbana       -7.413            8.102
#> Norma culta                13.743          -15.021

O sinal dos resíduos é importante para interpretar a associação entre as linhas e as colunas, ou entre a variável dependente e independente. Podemos visualizar melhor os resíduos por meio de uma matriz de correlação, com o pacote corrplot:

Podemos visualizar melhor os resíduos por meio de uma matriz de correlação, com o pacote corrplot:

library(corrplot)
#> corrplot 0.84 loaded
corrplot(resultadoP6$residuals, is.cor = FALSE)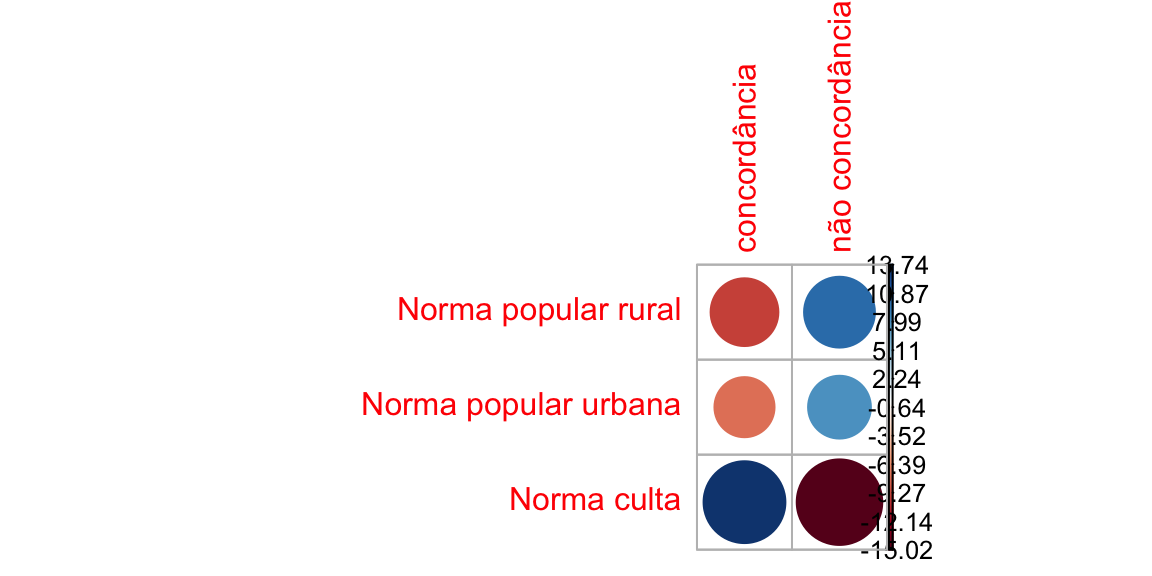

Nesta matriz de correlação, ou correlograma, o tamanho do círculo é proporcional à contribuição da célula para o efeito.

  • Resíduos positivos estão em azul e sinalizam uma associação positiva entre linha e coluna.
  • Resíduos negativos estão em vermelho e sinalizam uma associação negativa entre linha e coluna.

Podemos calcular o quanto cada célula contribui para o total do escore de qui-quadrado e dispor no correlograma:

contrib <- 100*resultadoP6$residuals^2/resultadoP6$statistic
round(contrib, 3)
#>                      concordância não concordância
#> Norma popular rural        12.175           14.544
#> Norma popular urbana        7.526            8.990
#> Norma culta                25.866           30.899
corrplot(contrib, is.cor = FALSE)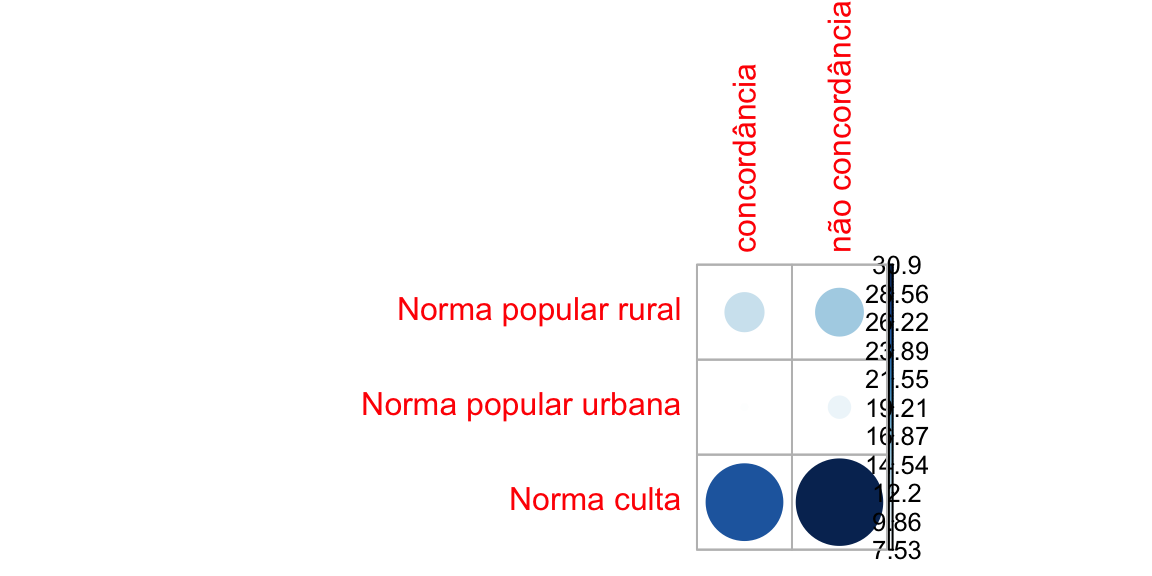

O nível “norma culta”’ é o que mais contribui para o resultado do teste.

Como fazer um teste de regressão a partir de uma tabela?

Primeiro, precisamos desfazer a tabela, retornando as ocorrências, para poder realizar uma análise de regressão. O preparo dos dados requer a conversão em um objeto data.frame.table e depois utilizar uma função que transforma as contagens em ocorrências counsToCases.

dados <- as.data.frame.table(dadosP6) ### converter a matriz em um data.frame
countsToCases <- function(x, countcol = "Freq") {  ###converter as contagens em ocorrências
  idx <- rep.int(seq_len(nrow(x)), x[[countcol]])
  x[[countcol]] <- NULL
  x[idx, ]
}
dados <- countsToCases(as.data.frame(dados))
names(dados) <- c("VI", "VD")  ## renomeando as colunas 
dados$VI <- factor(dados$VI, levels =c("Norma popular urbana", "Norma culta", "Norma popular rural")) ## reordenando os níveis
head(dados)  ##observar as 6 primeiras linhas
#>                      VI           VD
#> 1   Norma popular rural concordância
#> 1.1 Norma popular rural concordância
#> 1.2 Norma popular rural concordância
#> 1.3 Norma popular rural concordância
#> 1.4 Norma popular rural concordância
#> 1.5 Norma popular rural concordância

Agora os dados estão distribuídos por ocorrências, e não mais por contagem. Podemos realizar um outro tipo de teste, uma regressão logística generalizada (retome o material das outras aulas).

Vamos construir um modelo de regressão considerando que variável dependente é categórica nominal binária (com concordância ou sem concordância, em termos binários, 1 ou 0) e a variável preditora é também categórica.

modP6 <- glm(VD ~ VI, data = dados, family = "binomial")
summary(modP6)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.7506  -0.3539  -0.3539   0.6977   2.3672  
#> 
#> Coefficients:
#>                       Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)             0.9477     0.1080   8.776   <2e-16 ***
#> VINorma culta          -3.6870     0.1956 -18.845   <2e-16 ***
#> VINorma popular rural   0.3412     0.1575   2.166   0.0303 *  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 2114.5  on 1533  degrees of freedom
#> Residual deviance: 1275.0  on 1531  degrees of freedom
#> AIC: 1281
#> 
#> Number of Fisher Scoring iterations: 5

Um resultado 2.2e-16 está em notação científica e significa 2.2 x 10_-16_, ou seja, 0.00000000000000022, 15 zeros antes do ponto decimal.

A interpretação dos resultados considera o fato de que as chances de realização da variável são concordância ou não concordância.

O log das chances é uma função dos coeficientes estimados: P(ocorrer)/P(ocorrer) = β0 + β1x1 + β2x2 + … + βnxn em que P significa probabilidade de (ocorrer/não ocorrer), β0 é o intercepto, ponto do eixo em que a curva toca, β1 é o coeficiente das variáveis preditoras.

A tabela de coeficientes nos mostra uma estimativa para cada coeficiente (β) para o modelo de regressão logística. O coeficiente de uma variável preditora categórica é a mudança estimada no log natural das chances com o nível de referência o nível de coeficiente. Por padrão, os níveis são ordenados pela ordem alfabética (a mudança na ordem dos níveis do fator pode ser feita).

Coeficientes positivos indicam que o evento torna-se mais provável e coeficientes negativos indicam que o evento torna-se menos provável.

No exemplo, o nível de referência do intercepto é a realização com concordância e norma urbana popular. Na mudança de nível, o coeficiente para a ocorrência de não concordância na norma culta aumenta o log natural das chances em - 3.687 em relação à norma popular urbana, enquanto para a norma popular rural aumenta em 0.3412 em relação à norma popular urbana.

O valor do coeficiente não é em probabilidades, mas sim em log das razões de chance (log-odds).

  • Probabilidade: valor entre 0 e 1
  • Razão de chances (odds): valor de 0 ao ∞
  • Log de razão de chances (log-odds): de −∞ a ∞

Os resultados em log-odds permitem a comparação da magnitude dos coeficientes.

O que observar:

  • A ordem dos níveis das variáveis na saída (se não houve mudança, a ordenação dos níveis segue a ordem alfabética;
  • Os sinais dos coeficientes: se positivos ou negativos;
  • A magnitude dos coeficientes: a diferença entre eles;
  • O p-valor: a probabilidade que mede a evidência contrária à hipótese nula. P-valor baixo é uma forte evidência contra a hipótese nula.

Podemos visualizar os resultados do modelo em gráfico, utilizando o pacote ggstats.

library(ggstatsplot)
#> Registered S3 methods overwritten by 'broom.mixed':
#>   method         from 
#>   augment.lme    broom
#>   augment.merMod broom
#>   glance.lme     broom
#>   glance.merMod  broom
#>   glance.stanreg broom
#>   tidy.brmsfit   broom
#>   tidy.gamlss    broom
#>   tidy.lme       broom
#>   tidy.merMod    broom
#>   tidy.rjags     broom
#>   tidy.stanfit   broom
#>   tidy.stanreg   broom
#> Registered S3 methods overwritten by 'car':
#>   method                          from
#>   influence.merMod                lme4
#>   cooks.distance.influence.merMod lme4
#>   dfbeta.influence.merMod         lme4
#>   dfbetas.influence.merMod        lme4
ggstatsplot::ggcoefstats(x = modP6, exclude.intercept = FALSE, output = "plot")
#> Can't calculate log-loss.
#> New names:
#> * NA -> ...1
#> * NA -> ...2
#> * NA -> ...3
#> * NA -> ...4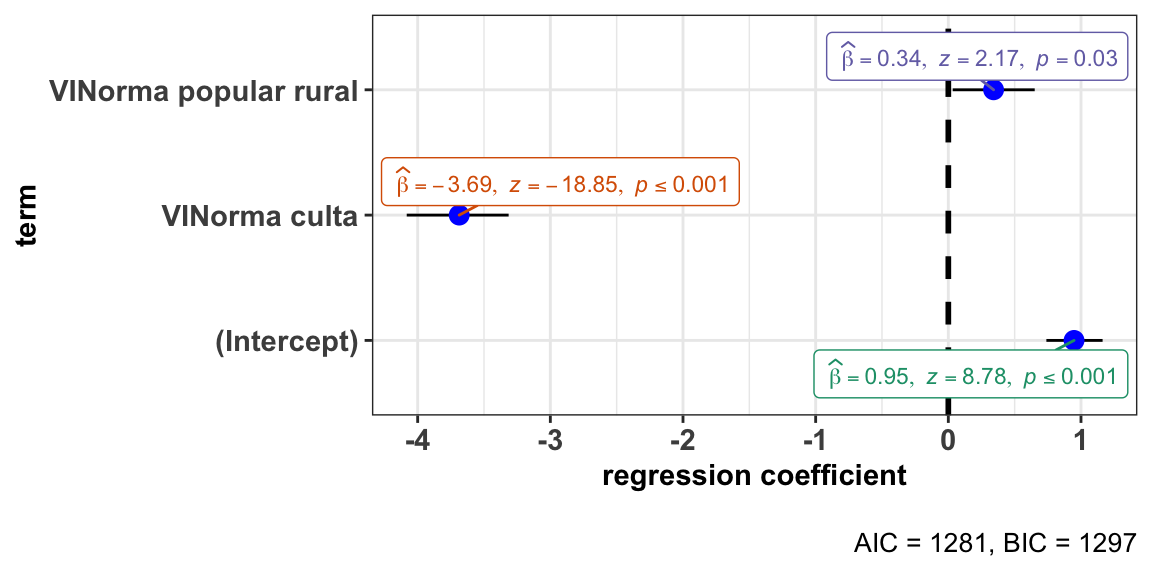

Nesta visualização, os resultados estão em log-odds (de −∞ a ∞).

Outra forma de visualização em gráfico pode ser produzida com o pacote sjPlot. Vejamos como ficam os resultados em razão de chances (odds):

library(sjPlot)
#> Install package "strengejacke" from GitHub (`devtools::install_github("strengejacke/strengejacke")`) to load all sj-packages at once!
plot_model(modP6)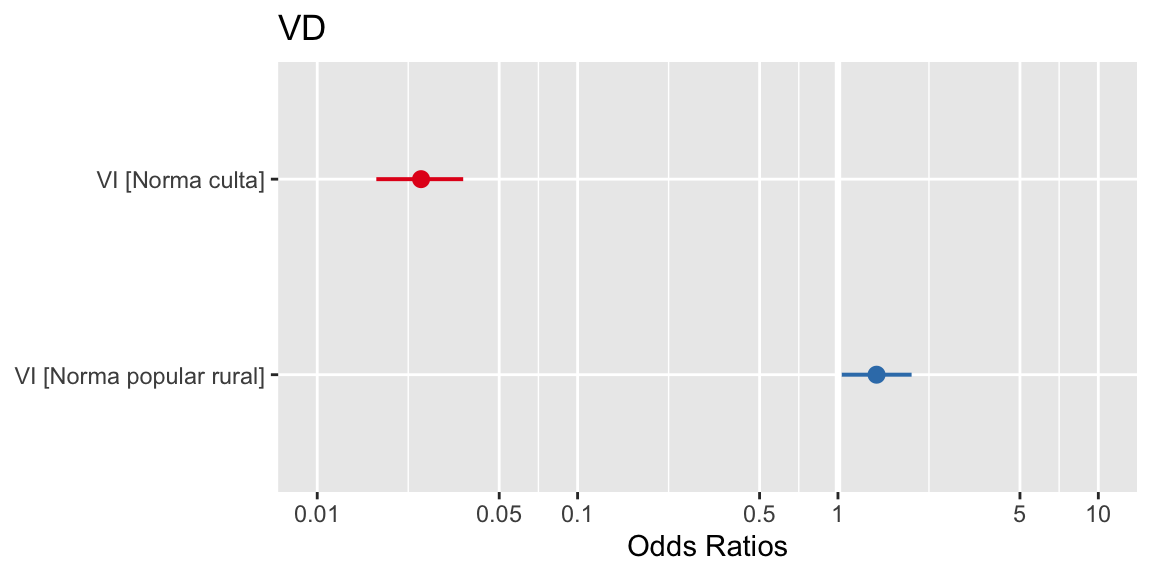

Embora “digam a mesma coisa”, os resultados em log-odds permitem observar a magnitude do efeito, daí por ser a forma preferível de reportar o resultado de um modelo de regressão generalizado.

Podemos também dispor os resultados em uma tabela formatável, com o pacote sjlabelled.

library(sjlabelled)
tab_model(modP6, transform = NULL, auto.label = FALSE)
  VD
Predictors Log-Odds CI p
(Intercept) 0.95 0.74 – 1.16 <0.001
VINorma culta -3.69 -4.08 – -3.31 <0.001
VINorma popular rural 0.34 0.03 – 0.65 0.030
Observations 1534
R2 Tjur 0.476

Como vimos, o teste do qui-quadrado, com a observação dos resíduos, apontou a contribuição do nível norma culta; o modelo de regressão construído explica de forma mais específica a atuação deste nível, estimando em log-odds a magnitude do efeito deste nível da variável independente na realização da variável dependente.

Os procedimentos para a análise univariada podem ser reproduzíveis mesmo sem se ter acesso ao conjunto de dados original. Este recurso pode auxiliar na produção de estudos de meta-análise, ao suprir resultados estatísticos nem sempre acessíveis e reportados nos estudos originais.

Como comparar estudos com conjuntos de dados distintos?

A direção do fenômento de variação na concordância verbal na terceira pessoa é a mesma em comunidades de fala distintas? Podemos responder a esta questão a partir de resultados apresentados em estudos anteriores, seguindo os procedimentos explicados anteriormente, e depois podemos proceder a uma meta-análise.

Concordância verbal na fala de Salvador e de Feira de Santana

Vamos realizar os procedimentos para comparar os resultados de Araujo (2013), concordância de terceira pessoa em função da idade em Feira de Santana, e de Souza (2011), concordância de terceira pessoa em função da idade em Salvador.

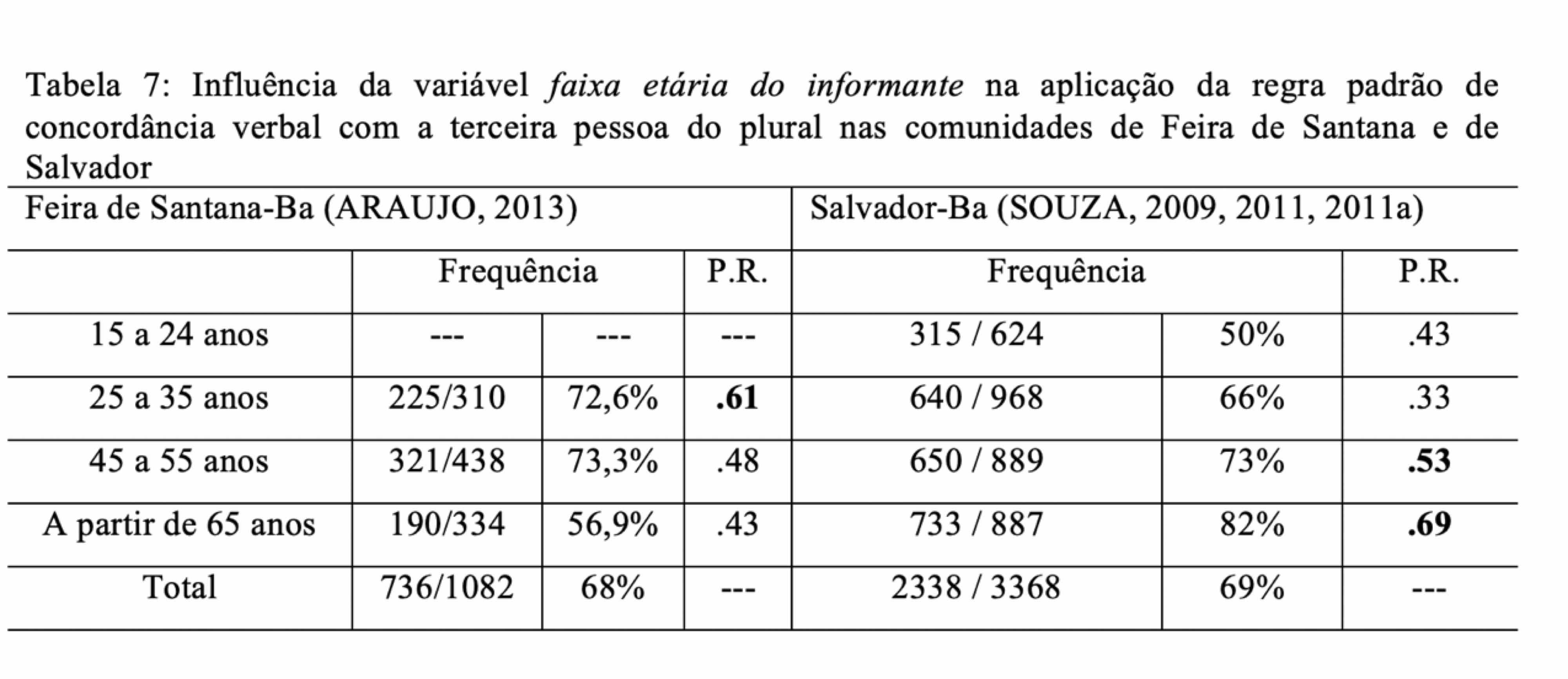
O teste aproximado para independência entre as proporções pode ser calculado:

prop.test(x = c(736, 2338), n = c(1082, 3368))
#> 
#>  2-sample test for equality of proportions with continuity correction
#> 
#> data:  c(736, 2338) out of c(1082, 3368)
#> X-squared = 0.68309, df = 1, p-value = 0.4085
#> alternative hypothesis: two.sided
#> 95 percent confidence interval:
#>  -0.04641901  0.01850159
#> sample estimates:
#>    prop 1    prop 2 
#> 0.6802218 0.6941805

O resultado não considera o efeito dos níveis da variável independente faixa etária, que foi controlada de maneira diferente nos dois estudos. Precisamos realizar análises univariadas para cada conjunto de dados e depois reuni-los.

Começamos por Feira de Santana:

  • Importar o conjunto de dados:
VD <- c("concordância", "não concordância")

VI <- c("25 a 35 anos", "45 a 55 anos", "mais de 65 anos")
dadosP6id <- data.matrix(rbind(
  c(225, 85),
  c(321,117),
  c(190, 144)
))
rownames(dadosP6id) <- VI
colnames(dadosP6id) <- VD
  • Realizar teste de qui-quadrado e observar os resíduos:
resultadoP6id <- chisq.test(dadosP6id)
resultadoP6id
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  dadosP6id
#> X-squared = 27.586, df = 2, p-value = 1.023e-06
corrplot(resultadoP6id$residuals, is.cor = FALSE)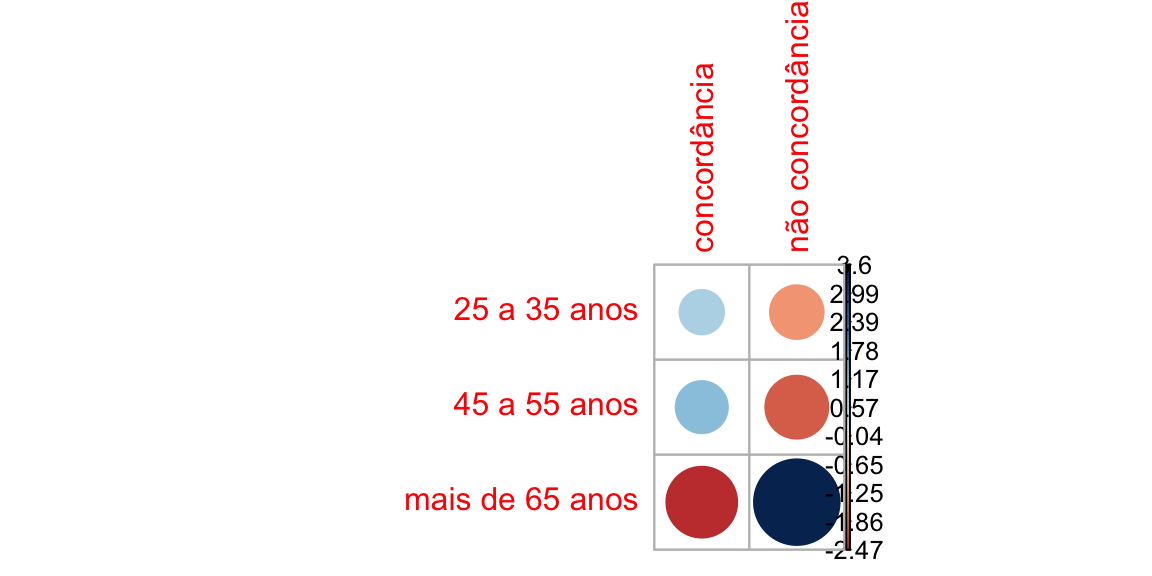

contrib <- 100*resultadoP6id$residuals^2/resultadoP6id$statistic
round(contrib, 3)
#>                 concordância não concordância
#> 25 a 35 anos           3.433            7.302
#> 45 a 55 anos           6.472           13.766
#> mais de 65 anos       22.073           46.953
corrplot(contrib, is.cor = FALSE)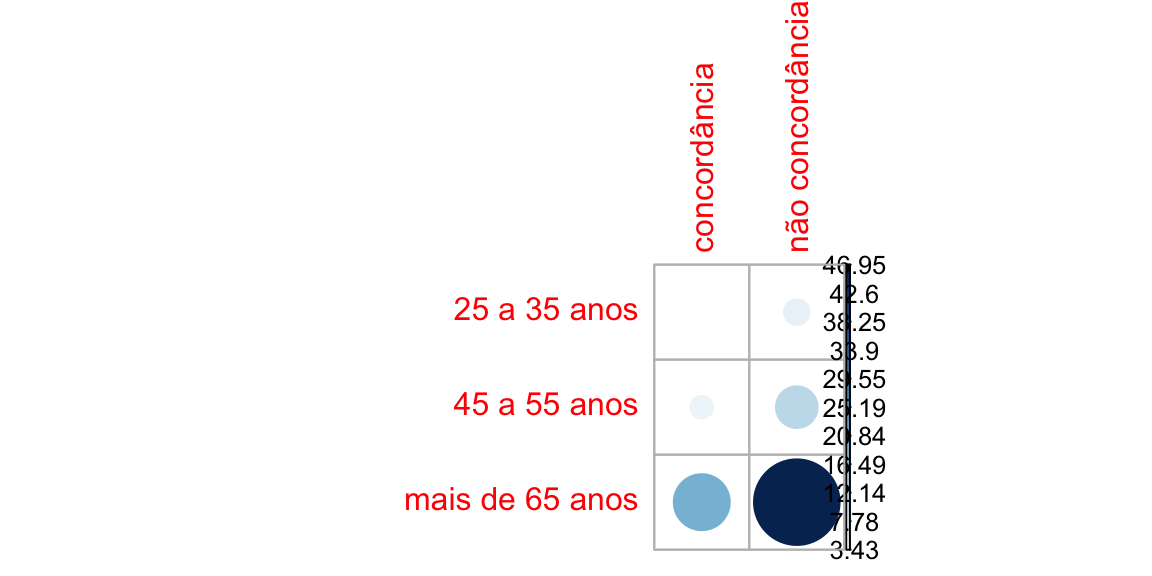

- Converter as contagens em ocorrências:

dados <- as.data.frame.table(dadosP6id)
dados <- countsToCases(as.data.frame(dados))
names(dados) <- c("VI", "VD") 
head(dados)
#>               VI           VD
#> 1   25 a 35 anos concordância
#> 1.1 25 a 35 anos concordância
#> 1.2 25 a 35 anos concordância
#> 1.3 25 a 35 anos concordância
#> 1.4 25 a 35 anos concordância
#> 1.5 25 a 35 anos concordância
  • Construir o modelo de regressão:
modP6fs <- glm(VD ~ VI, data = dados, family = "binomial")
summary(modP6fs)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.0622  -0.8006  -0.7884   1.2972   1.6248  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)       -0.97345    0.12732  -7.646 2.07e-14 ***
#> VI45 a 55 anos    -0.03582    0.16695  -0.215     0.83    
#> VImais de 65 anos  0.69624    0.16857   4.130 3.62e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 1356.2  on 1081  degrees of freedom
#> Residual deviance: 1329.3  on 1079  degrees of freedom
#> AIC: 1335.3
#> 
#> Number of Fisher Scoring iterations: 4
ggstatsplot::ggcoefstats(x = modP6fs, output = "plot")
#> Can't calculate log-loss.
#> New names:
#> * NA -> ...1
#> * NA -> ...2
#> * NA -> ...3
#> * NA -> ...4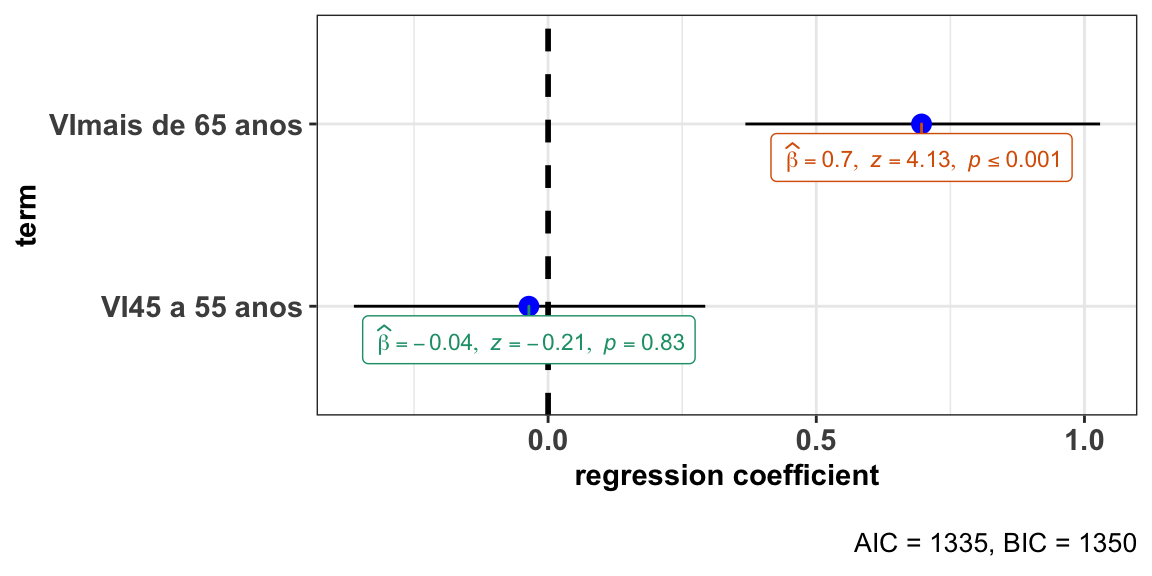

Agora, vamos realizar os mesmos procedimentos para Salvador:

  • Importar o conjunto de dados:
VD <- c("concordância", "não concordância")
VI <- c("15 a 24 anos", "25 a 35 anos", "45 a 55 anos", "mais de 65 anos")
dadosP6ssa <- data.matrix(rbind(
  c(315, 309),
  c(640,328),
  c(650, 239),
  c(733, 154)
))
rownames(dadosP6ssa) <- VI
colnames(dadosP6ssa) <- VD
  • Realizar teste de qui-quadrado e observar os resíduos:
resultadoP6ssa <- chisq.test(dadosP6ssa)
resultadoP6ssa
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  dadosP6ssa
#> X-squared = 189.13, df = 3, p-value < 2.2e-16
corrplot(resultadoP6ssa$residuals, is.cor = FALSE)

contrib <- 100*resultadoP6ssa$residuals^2/resultadoP6ssa$statistic
round(contrib, 3)
#>                 concordância não concordância
#> 15 a 24 anos          17.045           38.689
#> 25 a 35 anos           0.804            1.825
#> 45 a 55 anos           0.926            2.102
#> mais de 65 anos       11.807           26.802
corrplot(contrib, is.cor = FALSE)

  • Converter as contagens em ocorrências:
dados <- as.data.frame.table(dadosP6ssa)
dados <- countsToCases(as.data.frame(dados))
names(dados) <- c("VI", "VD") 
head(dados)
#>               VI           VD
#> 1   15 a 24 anos concordância
#> 1.1 15 a 24 anos concordância
#> 1.2 15 a 24 anos concordância
#> 1.3 15 a 24 anos concordância
#> 1.4 15 a 24 anos concordância
#> 1.5 15 a 24 anos concordância
  • Construir o modelo de regressão:
modP6ssa <- glm(VD ~ VI, data = dados, family = "binomial")
summary(modP6ssa)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.1692  -0.9097  -0.6176   1.1856   1.8713  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)       -0.01923    0.08007  -0.240     0.81    
#> VI25 a 35 anos    -0.64922    0.10499  -6.184 6.25e-10 ***
#> VI45 a 55 anos    -0.98128    0.11015  -8.908  < 2e-16 ***
#> VImais de 65 anos -1.54096    0.11945 -12.900  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 4147.5  on 3367  degrees of freedom
#> Residual deviance: 3958.4  on 3364  degrees of freedom
#> AIC: 3966.4
#> 
#> Number of Fisher Scoring iterations: 4
ggstatsplot::ggcoefstats(x = modP6ssa, output = "plot")
#> Can't calculate log-loss.
#> New names:
#> * NA -> ...1
#> * NA -> ...2
#> * NA -> ...3
#> * NA -> ...4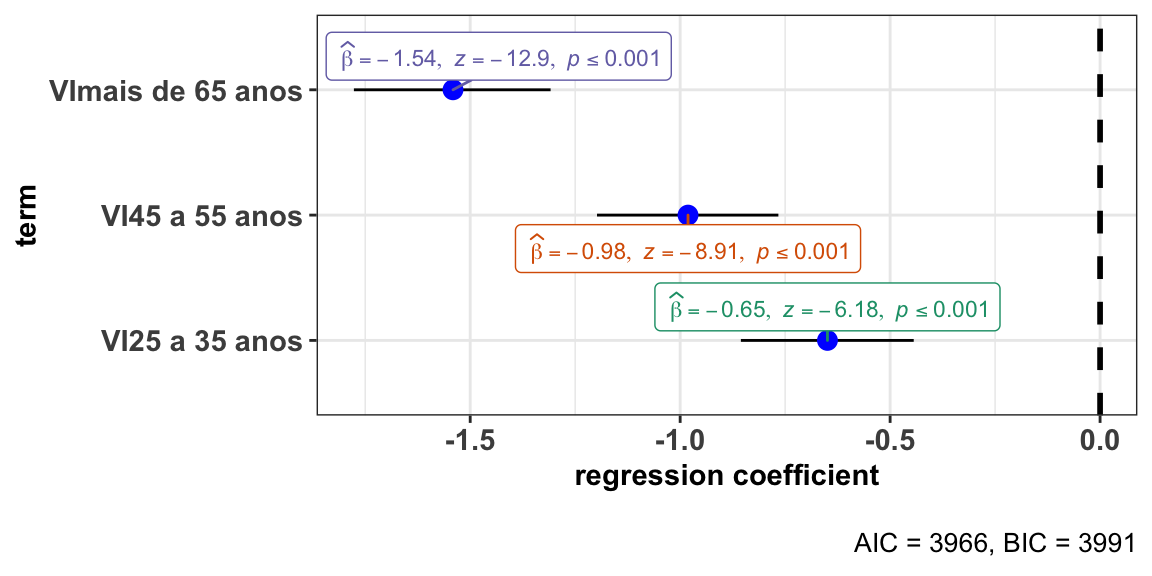

Podemos visualizar os dois modelos lado a lado em uma única tabela:

library(sjlabelled)
tab_model(modP6fs, modP6ssa, transform = NULL)
  VD VD
Predictors Log-Odds CI p Log-Odds CI p
(Intercept) -0.97 -1.23 – -0.73 <0.001 -0.02 -0.18 – 0.14 0.810
VI [45 a 55 anos] -0.04 -0.36 – 0.29 0.830 -0.98 -1.20 – -0.77 <0.001
VI [mais de 65 anos] 0.70 0.37 – 1.03 <0.001 -1.54 -1.78 – -1.31 <0.001
VI [25 a 35 anos] -0.65 -0.86 – -0.44 <0.001
Observations 1082 3368
R2 Tjur 0.025 0.056

Agora, vamos considerar os resultados para a fala popular de Feira de Santana e Salvador, também considerando a idade.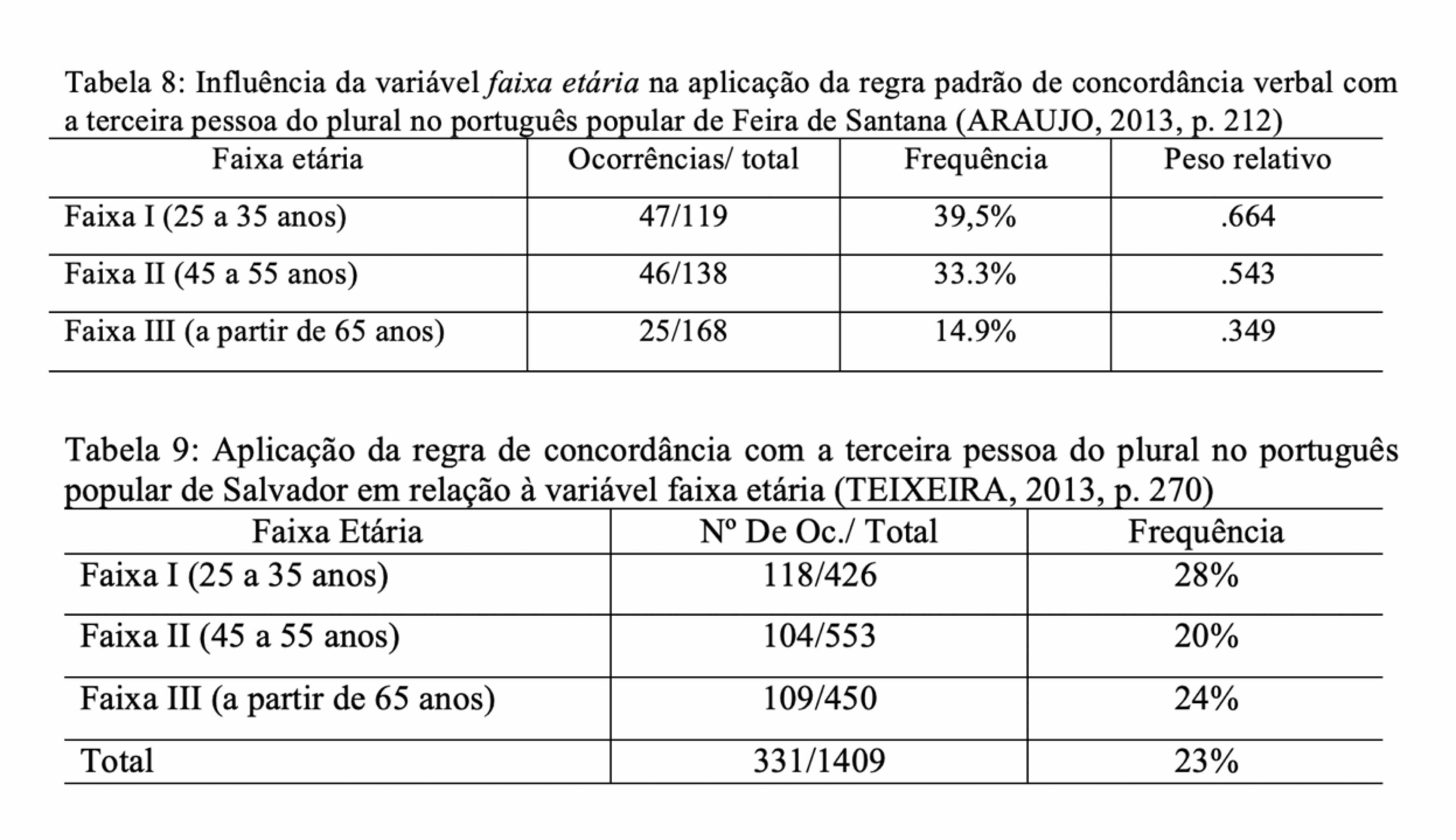

O teste aproximado para independência entre as proporções pode ser calculado:

prop.test(x = c(118, 331), n = c(425, 1409))
#> 
#>  2-sample test for equality of proportions with continuity correction
#> 
#> data:  c(118, 331) out of c(425, 1409)
#> X-squared = 2.9974, df = 1, p-value = 0.0834
#> alternative hypothesis: two.sided
#> 95 percent confidence interval:
#>  -0.006790312  0.092247666
#> sample estimates:
#>    prop 1    prop 2 
#> 0.2776471 0.2349184
  • O estudo de Araújo (2013) não fornece a linha de totais, o que requer usar a calculadora - sempre informe a linha de totais!

Vamos repetir os mesmos procedimentos anteriores para cada um dos conjuntos de dados. Começamos por Feira de Santana.

  • Importar o conjunto de dados:
VD <- c("concordância", "não concordância")
VI <- c("25 a 35 anos", "45 a 55 anos", "mais de 65 anos")
dadosP6fspop <- data.matrix(rbind(
  c(47, 72),
  c(46, 92),
  c(25, 143)
))
rownames(dadosP6fspop) <- VI
colnames(dadosP6fspop) <- VD
  • Realizar teste de qui-quadrado e observar os resíduos:
resultadoP6fspop <- chisq.test(dadosP6fspop)
resultadoP6fspop
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  dadosP6fspop
#> X-squared = 24.204, df = 2, p-value = 5.55e-06
corrplot(resultadoP6fspop$residuals, is.cor = FALSE)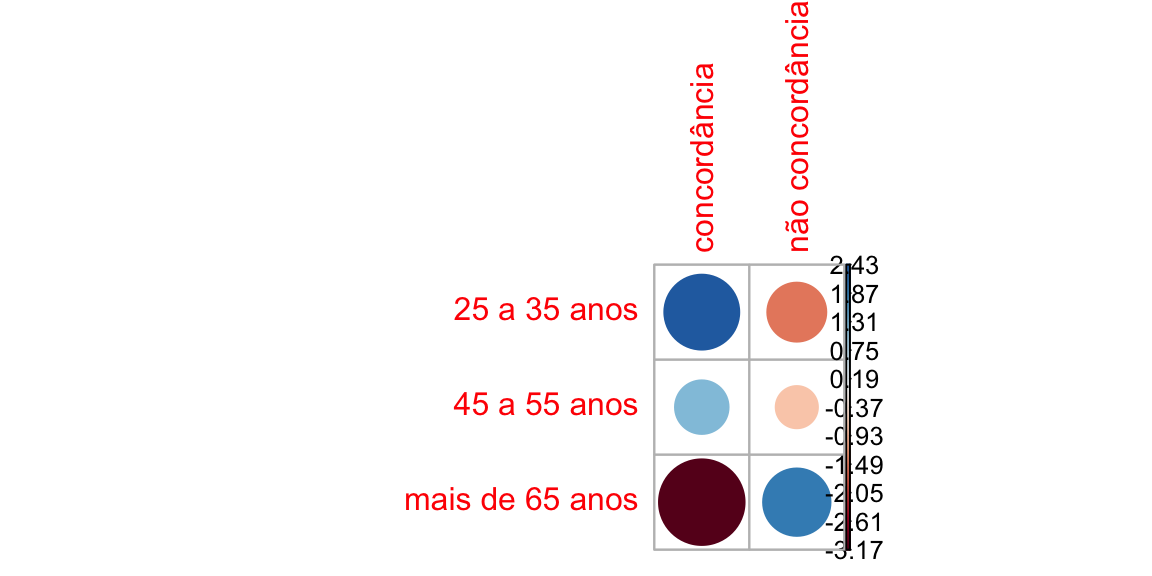

contrib <- 100*resultadoP6fspop$residuals^2/resultadoP6fspop$statistic
round(contrib, 3)
#>                 concordância não concordância
#> 25 a 35 anos          24.370            9.367
#> 45 a 55 anos           6.368            2.448
#> mais de 65 anos       41.498           15.950
corrplot(contrib, is.cor = FALSE)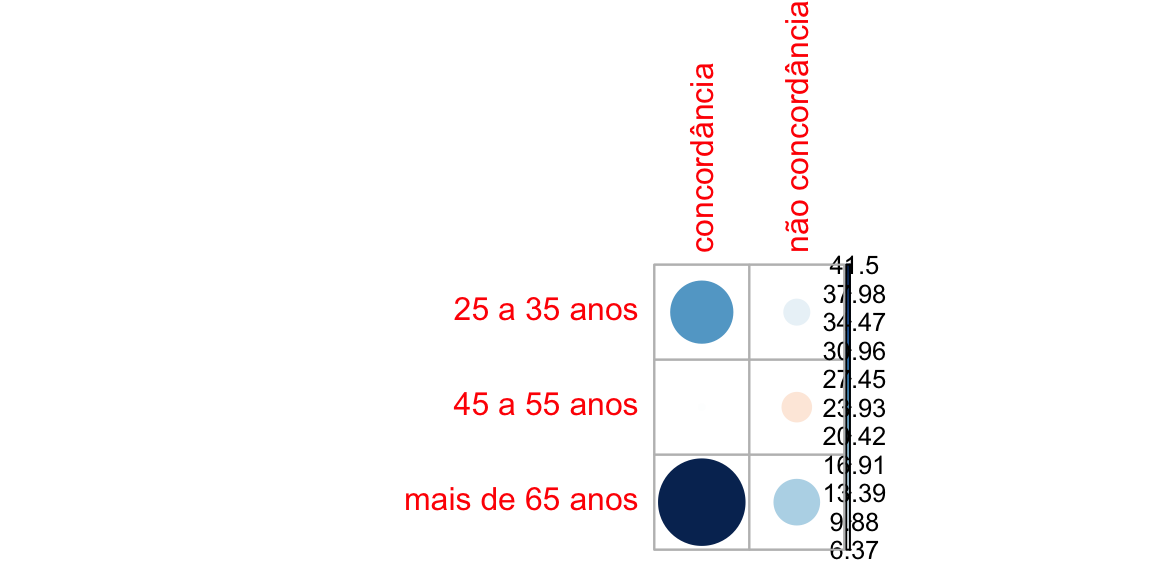

  • Converter as contagens em ocorrências:
dados <- as.data.frame.table(dadosP6fspop)
dados <- countsToCases(as.data.frame(dados))
names(dados) <- c("VI", "VD")
  • Construir o modelo:
modP6fspop <- glm(VD ~ VI, data = dados, family = "binomial")
summary(modP6fspop)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.9520  -1.3631   0.5677   0.9005   1.0025  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)         0.4265     0.1875   2.274   0.0229 *  
#> VI45 a 55 anos      0.2666     0.2603   1.024   0.3058    
#> VImais de 65 anos   1.3175     0.2866   4.596  4.3e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 502.11  on 424  degrees of freedom
#> Residual deviance: 476.69  on 422  degrees of freedom
#> AIC: 482.69
#> 
#> Number of Fisher Scoring iterations: 4
ggstatsplot::ggcoefstats(x = modP6fspop, output = "plot")
#> Can't calculate log-loss.
#> New names:
#> * NA -> ...1
#> * NA -> ...2
#> * NA -> ...3
#> * NA -> ...4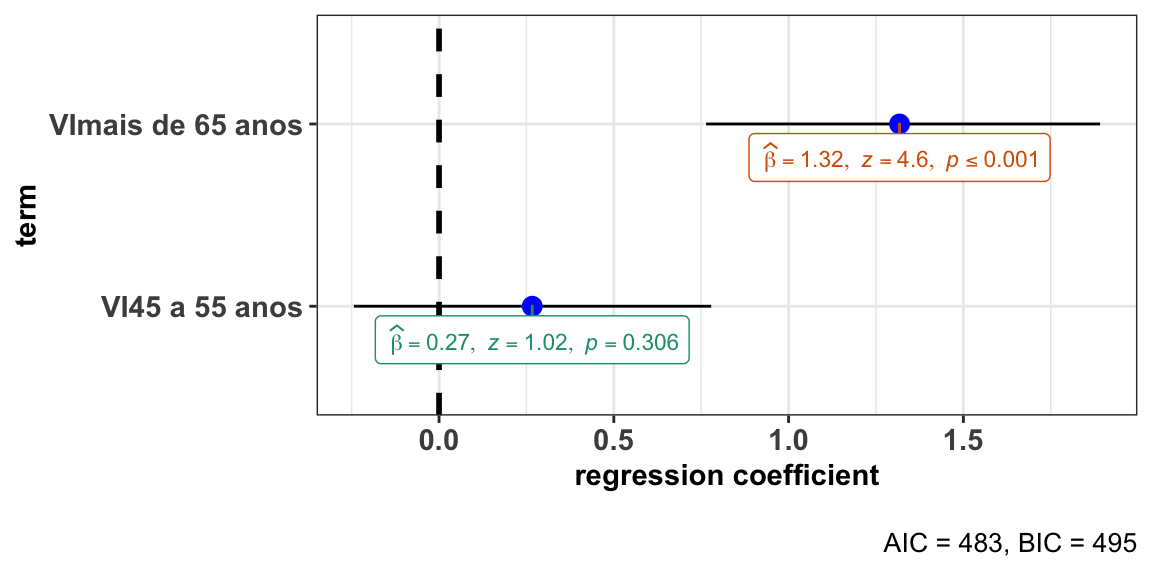

Idem para Salvador (Teixeira, 2013).

  • Importar o conjunto de dados:
VD <- c("concordância", "não concordância")
VI <- c("25 a 35 anos", "45 a 55 anos", "mais de 65 anos")
dadosP6ssapop <- data.matrix(rbind(
  c(118, 308),
  c(104, 449),
  c(109, 341)
))
rownames(dadosP6ssapop) <- VI
colnames(dadosP6ssapop) <- VD
  • Realizar teste de qui-quadrado e observar os resíduos:
resultadoP6ssapop <- chisq.test(dadosP6ssapop)
resultadoP6ssapop
#> 
#>  Pearson's Chi-squared test
#> 
#> data:  dadosP6ssapop
#> X-squared = 11.107, df = 2, p-value = 0.003875
corrplot(resultadoP6ssapop$residuals, is.cor = FALSE)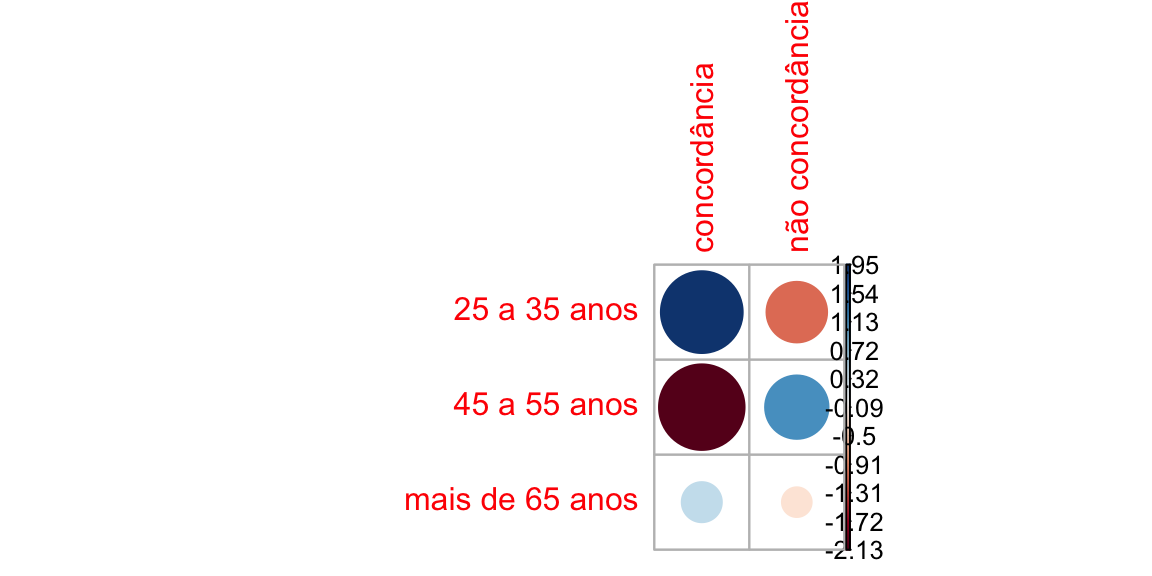

contrib <- 100*resultadoP6ssapop$residuals^2/resultadoP6ssapop$statistic
round(contrib, 3)
#>                 concordância não concordância
#> 25 a 35 anos          34.078           10.273
#> 45 a 55 anos          40.797           12.299
#> mais de 65 anos        1.962            0.592
corrplot(contrib, is.cor = FALSE)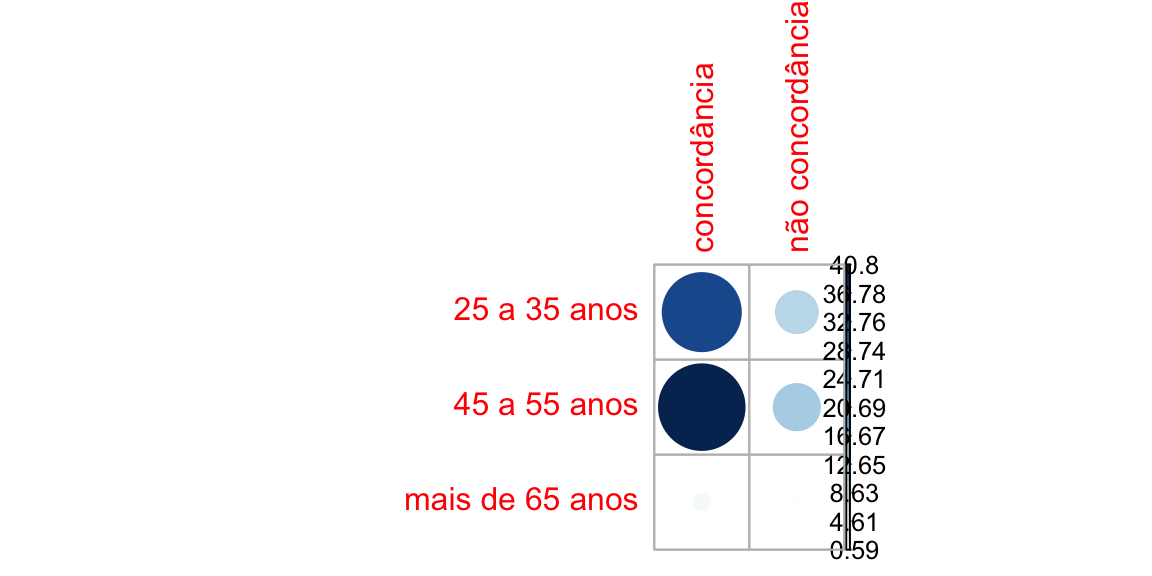

  • Converter as contagens em ocorrências:
dados <- as.data.frame.table(dadosP6ssapop)
dados <- countsToCases(as.data.frame(dados))
names(dados) <- c("VI", "VD")
  • Construir o modelo:
modP6ssapop <- glm(VD ~ VI, data = dados, family = "binomial")
summary(modP6ssapop)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.8281   0.6455   0.6455   0.7448   0.8054  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)         0.9594     0.1083   8.862  < 2e-16 ***
#> VI45 a 55 anos      0.5032     0.1535   3.278  0.00104 ** 
#> VImais de 65 anos   0.1811     0.1544   1.173  0.24066    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 1546.9  on 1428  degrees of freedom
#> Residual deviance: 1535.7  on 1426  degrees of freedom
#> AIC: 1541.7
#> 
#> Number of Fisher Scoring iterations: 4
ggstatsplot::ggcoefstats(x = modP6ssapop, output = "plot")
#> Can't calculate log-loss.
#> New names:
#> * NA -> ...1
#> * NA -> ...2
#> * NA -> ...3
#> * NA -> ...4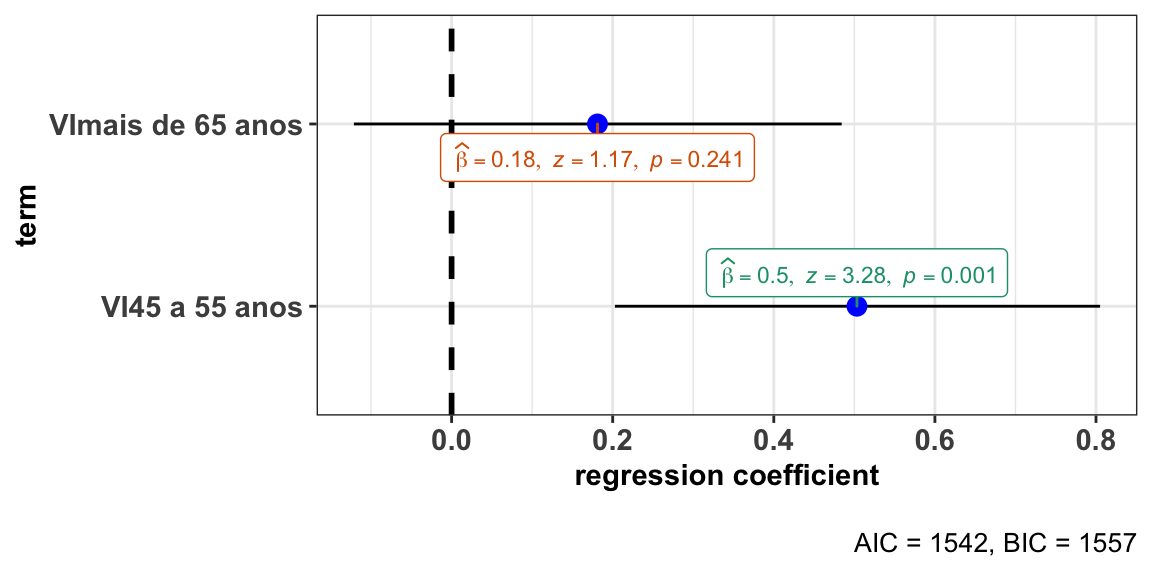

Novamente, podemos sumarizar os modelos em uma mesma tabela:

library(sjlabelled)
tab_model(modP6fspop, modP6ssapop, transform = NULL)
  VD VD
Predictors Log-Odds CI p Log-Odds CI p
(Intercept) 0.43 0.06 – 0.80 0.023 0.96 0.75 – 1.18 <0.001
VI [45 a 55 anos] 0.27 -0.24 – 0.78 0.306 0.50 0.20 – 0.81 0.001
VI [mais de 65 anos] 1.32 0.76 – 1.89 <0.001 0.18 -0.12 – 0.48 0.241
Observations 425 1429
R2 Tjur 0.057 0.008

Meta-análise

Como ficam todos os estudos no mesmo modelo? EVamos construir uma visualização de regressão com os parâmetros dos quatro estudos anteriores.

library(sjlabelled)
summary(modP6fs)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.0622  -0.8006  -0.7884   1.2972   1.6248  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)       -0.97345    0.12732  -7.646 2.07e-14 ***
#> VI45 a 55 anos    -0.03582    0.16695  -0.215     0.83    
#> VImais de 65 anos  0.69624    0.16857   4.130 3.62e-05 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 1356.2  on 1081  degrees of freedom
#> Residual deviance: 1329.3  on 1079  degrees of freedom
#> AIC: 1335.3
#> 
#> Number of Fisher Scoring iterations: 4
summary(modP6fspop)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.9520  -1.3631   0.5677   0.9005   1.0025  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)         0.4265     0.1875   2.274   0.0229 *  
#> VI45 a 55 anos      0.2666     0.2603   1.024   0.3058    
#> VImais de 65 anos   1.3175     0.2866   4.596  4.3e-06 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 502.11  on 424  degrees of freedom
#> Residual deviance: 476.69  on 422  degrees of freedom
#> AIC: 482.69
#> 
#> Number of Fisher Scoring iterations: 4
summary(modP6ssa)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.1692  -0.9097  -0.6176   1.1856   1.8713  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)       -0.01923    0.08007  -0.240     0.81    
#> VI25 a 35 anos    -0.64922    0.10499  -6.184 6.25e-10 ***
#> VI45 a 55 anos    -0.98128    0.11015  -8.908  < 2e-16 ***
#> VImais de 65 anos -1.54096    0.11945 -12.900  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 4147.5  on 3367  degrees of freedom
#> Residual deviance: 3958.4  on 3364  degrees of freedom
#> AIC: 3966.4
#> 
#> Number of Fisher Scoring iterations: 4
summary(modP6ssapop)
#> 
#> Call:
#> glm(formula = VD ~ VI, family = "binomial", data = dados)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -1.8281   0.6455   0.6455   0.7448   0.8054  
#> 
#> Coefficients:
#>                   Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)         0.9594     0.1083   8.862  < 2e-16 ***
#> VI45 a 55 anos      0.5032     0.1535   3.278  0.00104 ** 
#> VImais de 65 anos   0.1811     0.1544   1.173  0.24066    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 1546.9  on 1428  degrees of freedom
#> Residual deviance: 1535.7  on 1426  degrees of freedom
#> AIC: 1541.7
#> 
#> Number of Fisher Scoring iterations: 4

São dois procedimentos: o primeiro é construir um data.frame com os parâmetros de cada modelo; depois, gerar a visualização dos resultados em um único eixo. > o procedimento de construção do data.frame, neste momento, será manual (copie os valores em cada um dos vetores; o processo pode ser automatizado, mas eu ainda não consegui aplicar uma função para isso)

### Construtir o data.frame
df <-
  structure(
    list(
      term = structure(
        1:4,
        .Label = c("Feira de Santana \n (Araújo, 2013)", "Feira de Santana, Popular \n (Araújo, 2013)", "Salvador \n (Souza, 2009)", "Salvador, Popular \n (Teixeira, 2013)"),
        class = "factor"
      ),
      estimate = c(
        -0.97345,
        0.4265,
        -0.01923,
        0.9594
      ),
      std.error = c(
        0.12732,
        0.1875,
        0.08007,
        0.1083
      ),
      statistic = c(
        -7.646,
        2.274,
        -0.240,
        8.862 
      ),
      p.value = c(
        2.07e-14,
        0.0229,
        0.81,
        2e-16
      ),
      df.residual = c(
        1079,
        422,
        3364,
        422
      )
    ),
    row.names = c(NA, -4L),
    class = c("tbl_df", "tbl", "data.frame")
  )
### gerar a visualização gráfica:
ggstatsplot::ggcoefstats(
  x = df,
  statistic = "z",
  sort = "ascending",
  title = "Concordância padrão em P6",
  ylab = "Amostras",
  xlab = "Coeficiente de regressão",
  caption = "Meta-análise"
)

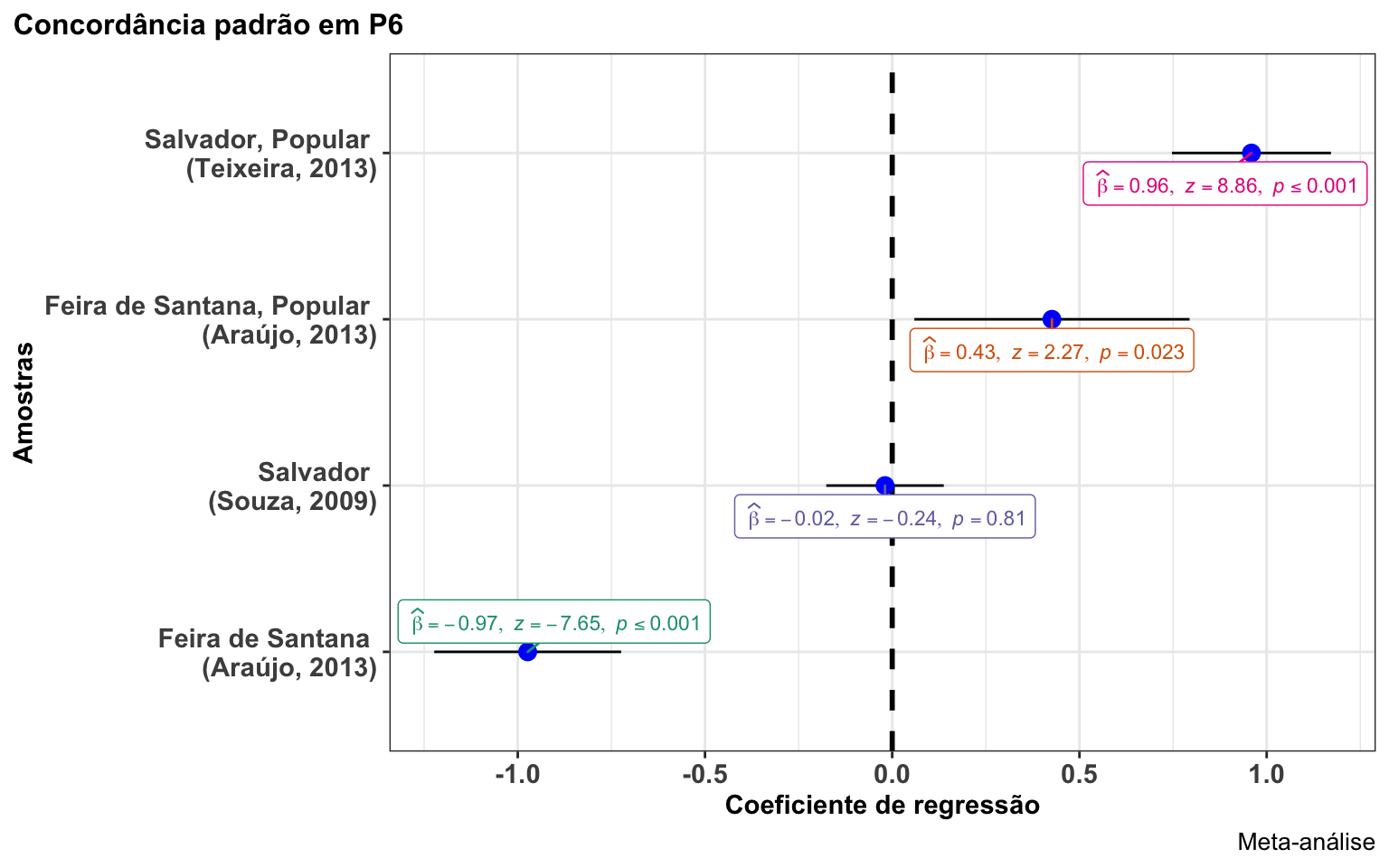
Agora os modelos podem ser comparados! As amostras de fala popular tanto de Salvador como de Feira de Santana são as que mais tendem à não concordância (nível de referência = concordância; os resultados devem ser interepretados em relação à contraparte do valor de referência). A amostra de fala não popular de Salvador não é estatisticamente significativa, e a fala não popular de Feira de Santana tende a realização da concordância (o coeficiente é negativo para a não concordância).

Uma representação apenas com os percentuais para esta relação foi apresentada na primeira versão do manuscrito:

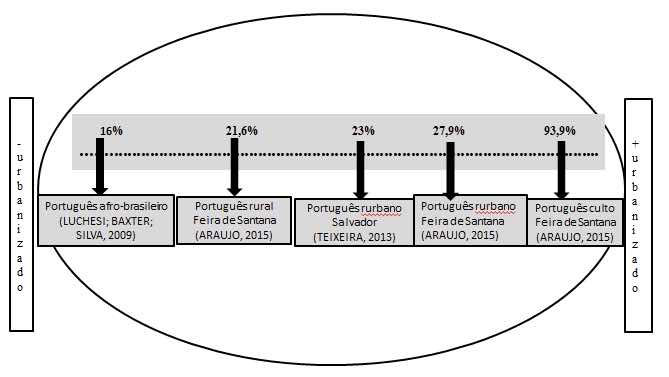
O problema de considerar apenas os percentuais é que a distribuição pode não ser estatisticiamente sigificativa, como foi o caso da fala não popular de Salvador. A meta-análise dá segurança e suporte para a generalização de resultados, e neste caso, para a validação da tendência geral da direção de mudança.

  • Confira sempre os números! Um erro e todo o resultado é modificado.

Este tutorial foi útil para subsidiar estudos que produziram argumentos baseados em meta-análise, como Análise contrastiva da estrutura do sintagma nominal possessivizado no português brasileiro e A variável sexo/gênero no português falado no sertão alagoano. Se você também usou em seu trabalho, compartilhe comigo!

Como citar:

FREITAG, Raquel M. K. Como fazer meta-análise com dados sociolinguísticos?. Disponível em: https://rkofreitag.github.io/meta.html/. Atualizado em: 2021-04-11.